Question

How do you find the area inside one loop of the lemniscate `r^2=5sin2theta`?

Answer 1

From the reference Area with Polar Coordinates, we obtain the following formula:

`A = 1/2int_alpha^beta r^2 d theta`

Explanation:

Here is a graph of `r = sqrt(5sin(2theta))`

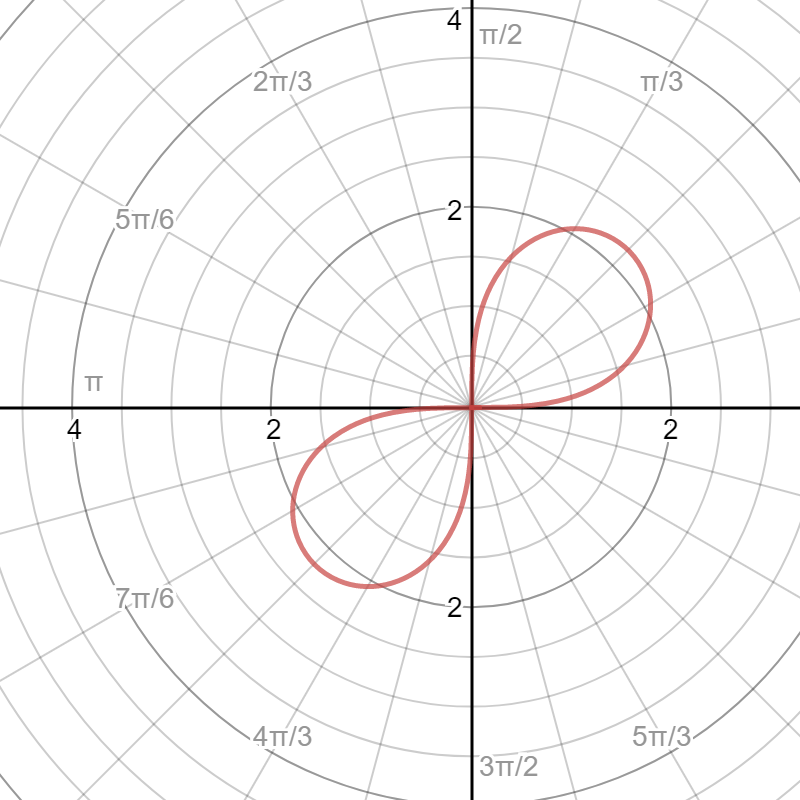
It is easy to see that one loop goes `theta` goes from `0` to `pi/2`

Therefore, the integral is:

`A = 1/2int_0^(pi/2) 5sin(2theta) d theta`

The indefinite integral of this is:

`1/2int sin(2theta) d theta = -5/4cos(2theta) + C`

Evaluating at the limits:

`A = -5/4(cos(pi)-cos(0))`

`A = 5/2`