Question

How do you find the area inside the oval limaçon `r=8+3costheta`?

Answer 1

`137/2pi`

Explanation:

We have:

`r = 8+3cos theta`

Here is the graph of the curves. The shaded area, `A`, is the area of interest:

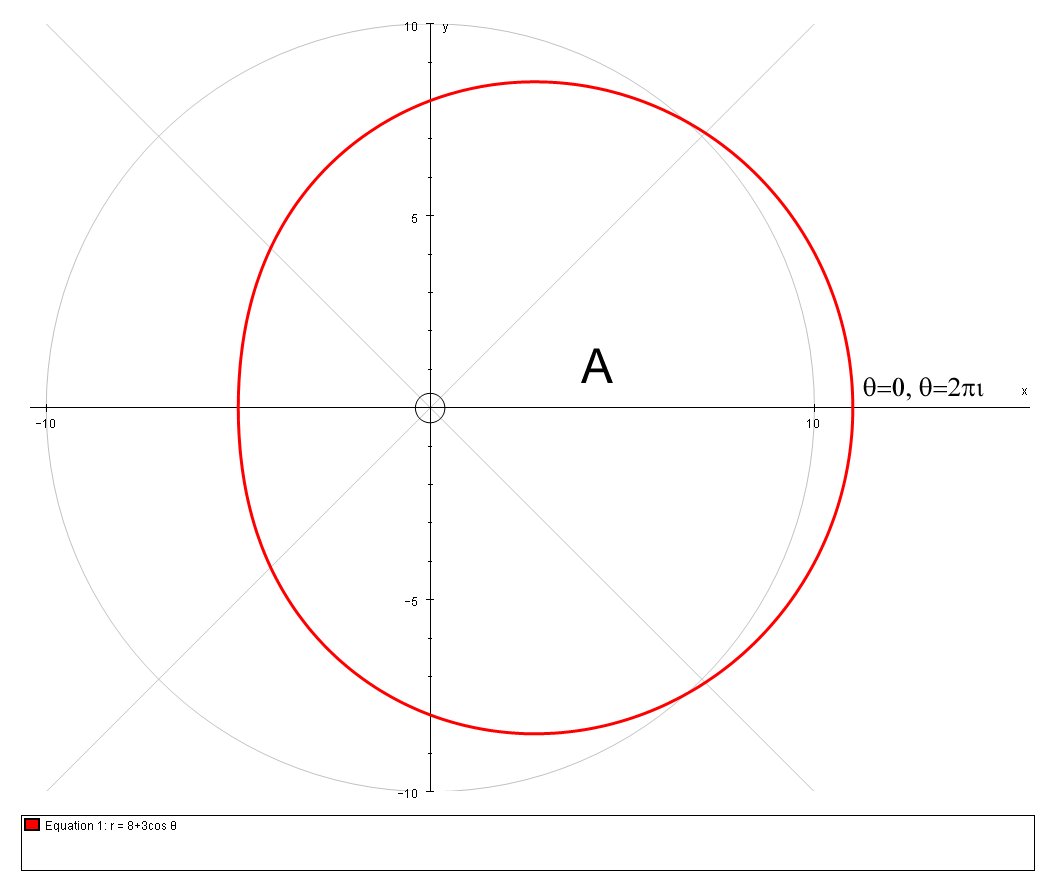
And we calculate the area of the segment `A`, via Calculus using the polar form for area:

`A = int_alpha^beta 1/2r^2 \ d theta`

Thus:

`A = 1/2 \ int_0^(2pi) 1/2(8+3cos theta) \ d theta`
`\ \ = 1/2 \ int_0^(2pi) (64+48costheta+9cos^2theta ) \ d theta`
`\ \ = 1/2 \ int_0^(2pi) 64+48costheta+9/2(1+cos2theta ) \ d theta`
`\ \ = 1/4 \ int_0^(2pi) 128+96costheta+9(1+cos2theta ) \ d theta`
`\ \ = 1/4 \ int_0^(2pi) 137+96costheta+9cos2theta \ d theta`
`\ \ = 1/4 \ [137 theta+96sintheta+9/2sin2theta ]_0^(2pi)`
`\ \ = 1/4 \ {(274pi+0+0) - (0+0+0)`
`\ \ = 137/2pi`