Question

How do you find the area of a trapezoid when you have the length of every side but not the height?

Answer 1

Let's say that you have the length of every side and they are named `a`, `b`, `c` and `d` like in my drawing, with `b` and `d` being base sides and `d` being the longer base.

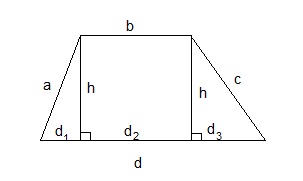
The formula to compute the area of trapezoid is:

`A = (b+d)/2 * h`,

so basically the only thing we need to do is computing `h`.

If you draw the height `h` like in my drawing, you see that the long base `d` can be divided into three intervals: `d = d_1 + d_2 + d_3` with `d_2 = b` and `d_1` and `d_3` yet unknown.

However, we also have two right angle triangles, one with the legs `d_1` and `h` and the hypotenuse `a` and one with the legs `d_3` and `h` and the hypotenuse `c`.

So, we know three things (with the known values marked in `color(green)(green)`):

1. `color(white)(xxx) d_1 + d_3 = color(green)(d) - color(green)(b)`

2. `color(white)(xxx) d_1 ^2 + h^2 = color(green)(a^2)` (theorem of Pythagoras)

3. `color(white)(xxx) d_3^2 + h^2 = color(green)(c^2)` (theorem of Pythagoras)

Now, you can solve the equation in 1. for e.g. `d_1` and plug it into equation 2. or 3.

Afterwards, the equations can be solved, and you will get the values for `d_1`, `d_3` and `h`.

And as soon as you have `h`, you can appy the formula and compute the area!

Please also check here an example where I've done exactly the same calculation on concrete values. :-)

http://socratic.org/questions/what-is-the-area-of-a-trapezoid-with-base-lengths-of-12-and-40-and-side-lengths-#193240