How do you find the area of a triangle from the co-ordinates of its vertices, without having to calculate the length of the triangles sides?
2 Answers
See below.
Explanation:
Finding the area of a triangle from its co-ordinates.
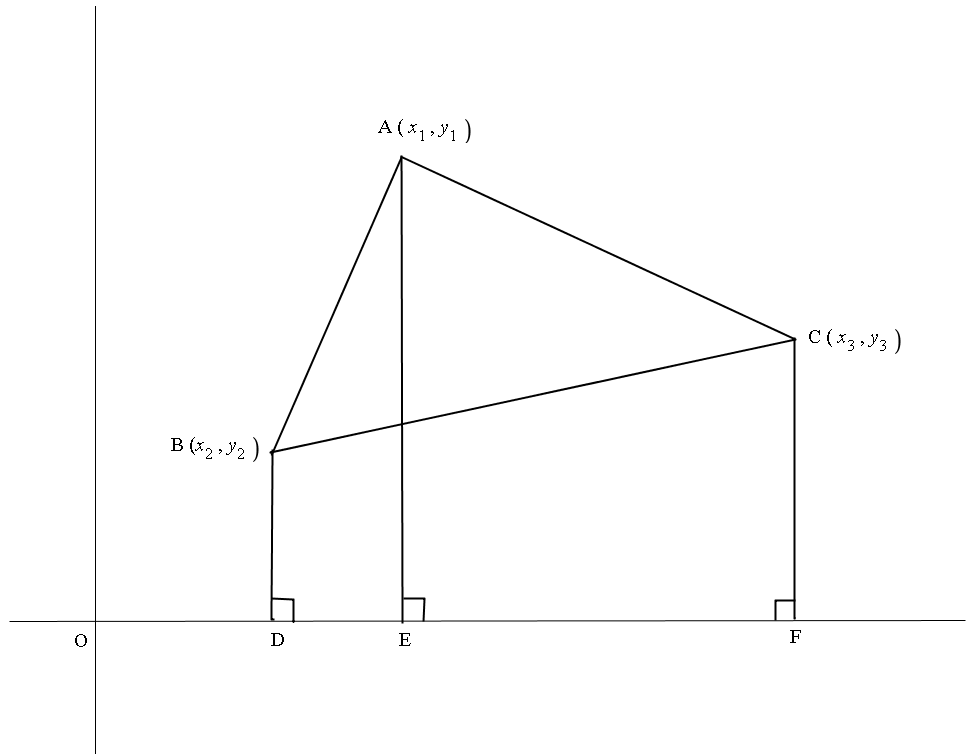
Using diagram.
We are looking for area of
We form perpendiculars BD, AD and CF to the x axis.
We then notice that:
Factor out
Collect terms containing
Terms containing
Terms containing
We now have a formula:
The absolute bars ensure that the area will be positive, whatever order we take them in.
This is a much better method than calculating the length of the sides, which invariably will be in surd form, making further calculations difficult. There isn't a lot of information on this and similar methods, and the reason for answering my own question was to show this method. I have to give credit to contributors Dean R and Binyaka C for pointing me in the direction of this and similar methods.
A triangle with vertices
We can also write it as
Explanation:
Let's imagine a triangle with vertices
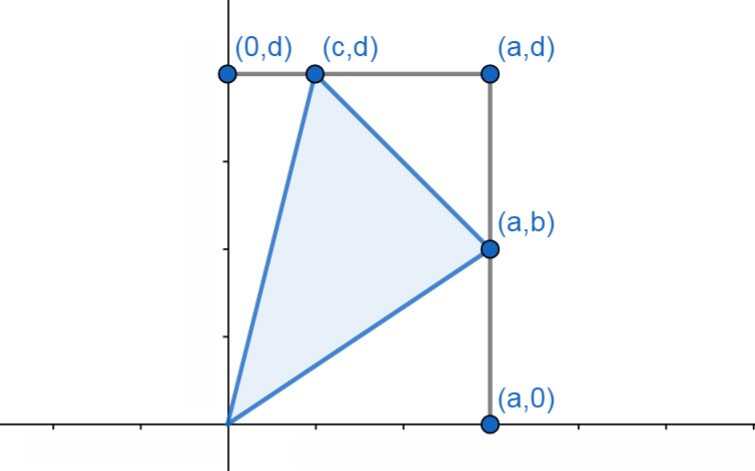
The triangle's area
The area is half the cross product. This is the signed area; if we had taken the points in the other order we'd get negative the area.
For an arbitrary triangle we translate
We substitute
That's one of our formulas. Multiplying it out, we get the standard form of the Shoelace Formula,
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
When we have three or more dimensions for the vertices we should do it this way:
Given vertices
but I won't derive that one now.


