The polar curve #r=2-sin theta#, #0 le theta < 2pi# looks like this.
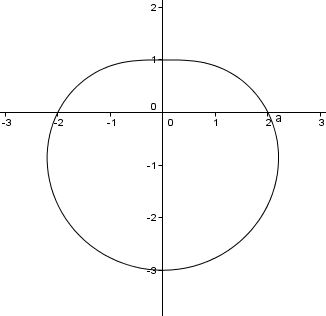
we can find the area #A# of the enclosed region can be found by
#A=int_0^{2pi}\int_0^{2-sin theta}r dr d theta={9pi}/2#
Let us evaluate the double integral above.
#A=int_0^{2pi}\int_0^{2-sin theta}r dr d theta#
#=int_0^{2pi}[r^2/2]_0^{2-sin theta} d theta#
#=1/2int_0^{2pi}(2-sin theta)^2 d theta#
#=1/2int_0^{2pi}(4-4sin theta+ sin^2 theta) d theta#
by #sin^2 theta=1/2(1-cos 2theta)#,
#=1/2int_0^{2pi}(9/2-4sin theta-1/2cos2theta)d theta#
#=1/2[9/2theta+4cos theta-1/4sin2theta]_0^{2pi}#
#=1/2[9pi+4-0-(0+4-0)]={9pi}/2#

