Question

How do you find the area under the curve `y=4 -x^2` with 6 rectangles over [-2,1] by using the LHS rule?

Answer 1

`LRS = 8.125`

Explanation:

We have:

`f(x) = 4-x^2`

We want to calculate over the interval `[1,5]` with `4` strips; thus:

`Deltax = (1-(-2))/6 = 0.5`

Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;

Left Riemann Sum

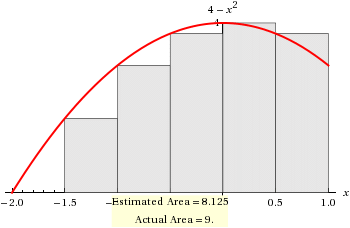
`LRS = sum_("left")f(x)Deltax`
`" " = Deltax { f(-2)+f(-1.5) + f(-1) + f(-0.5) + f0) + f0.5) } \ \ \` (The LHS values)
`" " = 0.5*(0+1.75+3+3.75+4+3.75)`
`" " = 0.5*16.25`
`" " = 8.125`

Actual Value

For comparison of accuracy:

`Area = int_-2^1 \ 4-x^2 \ dx`
`" " = [4x-x^3/3]_-2^1`
`" " = {(4-1/3)-(-8+8/3)}`
`" " = {(11/3)-(-16/3)}`
`" " =9`