How do you find the area using the trapezoidal approximation method, given #(5t + 6) dt #, on the interval [3, 6] with n=4?
1 Answer
Explanation:
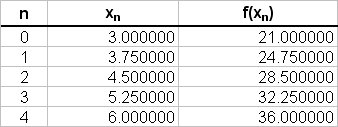
The values of
Using the trapezoidal rule:
# int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}#
We have:
# int_(3)^(6) \ 5t+6 \ dt ~~ 0.75/2 { (21 + 36) + " #
# " " 2(24.75 + 28.5 + 32.25) }#
# " " = 0.375 { + 57 + 2(85.5) }#
# " " = 0.375 { + 57 + 171 }#
# " " = 0.375 { + 228 }#
# " " = 85.5#
It is always worth thinking about the interpretation of a mathematical question and/or result. In this case we are being asked to find the area under a straight line, which will be a trapezium
graph{5x+6 [-3, 8, -5, 55]}
So we can calculate the exact area:
# A= (1/2)(21+36)(3) = 85.5#
It is no coincidence that the above trapezium rule calculation gave us the exact result, because obviously the rule estimates the area of integration with small width trapeziums. In the case of a straight line those trapeziums are exact.