How do you find the area using the trapezoidal approximation method, given #cos(4 x) dx#, on the interval [-1, 2] with n=10?
1 Answer
# int_(-1)^2 \ cos4x \ dx ~~ 0.0510 # 4dp
Explanation:
We have:
# y = cos(4x) #
We want to estimate
# Deltax = (2-(-1))/10 = 0.3#
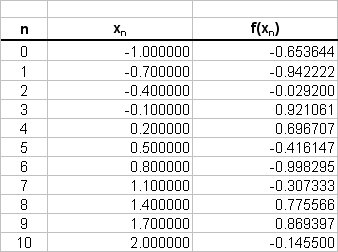
The values of the function are tabulated as follows;
Trapezium Rule
# A = 0.3/2 * { -0.653644 - 0.1455 + #
# \ \ \ \ \ \ \ \ \ 2*(-0.942222 - 0.0292 + 0.921061 + #
# \ \ \ \ \ \ \ \ \ 0.696707 - 0.416147 - 0.998295 - #
# \ \ \ \ \ \ \ \ \ 0.307333 + 0.775566 + 0.869397) } #
# \ \ \ = 0.15 * { -0.799144 + 2*(0.569535) } #
# \ \ \ = 0.15 * { -0.799144 + 1.139069 } #
# \ \ \ = 0.15 * 0.339926 #
# \ \ \ = 0.050989 #
Actual Value
For comparison of accuracy:
# A= int_(-1)^2 \ cos4x \ dx #
# " \ \ \ = [1/4sin4x]_(-1)^2 #
# " \ \ \ = 1/4(sin8-sin(-4)) \ \ \ \ # (radians!)
# " \ \ \ = 1/4(0.989358... - 0.756802 ...) #
# " \ \ \ = 0.058138 ... #