How do you find the area using the trapezoidal approximation method, given #cos(x^2)#, on the interval [0, 1] with n=8?
1 Answer
Dec 18, 2016
and so we can conclude that
Explanation:
The values of
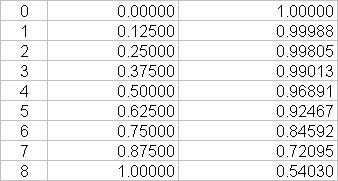
Using the trapezoidal rule:
# int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}#
We have:
# int_(0)^(1) cos(x^2)dx ~~ 0.125/2 { 1 + 0.5403#
# " " + 2(0.99988 + 0.99805 + 0.99013 #
# " " + 0.96891 + 0.92467 + 0.84592 #
# " " + 0.72095)}#
# " " = 0.0625 { 1.5403 + 2( 6.44851 )}#
# " " = 0.0625 { 1.5403 + 12.89702 }#
# " " = 0.0625 { 14.43733 }#
# " " = 0.90233#
and so we can conclude that

