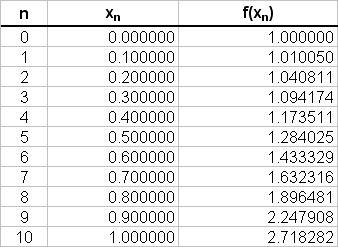
How do you find the area using the trapezoidal approximation method, given #e^(x^2)#, on the interval [0,1] with n=10?
1 Answer
# int_0^1 e^(x^2) \ dx ~~ 1.4672 # (4dp)
Explanation:
The values of
The Trapezium Rule:
# int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}#
uses a series of two consecutive ordinates and a best fit straight line to form trapeziums to approximate the area under a curve, It will have 100% accuracy if
So,
# int_0^1 e^(x^2) \ dx ~~ 0.1/2 { (1 + 2.718281) + #
# " " 2(1.01005 + 1.04081 + 1.094174 + 1.17351 + 1.284025 +#
# " " 1.433329 + 1.632316 + 1.89648 + 2.247907) } #
# " "= 0.05 { + 3.718281 + 2(12.812606) } #
# " "= 0.05 { + 3.718281 + 25.625212 }#
# " "= 0.05 { + 29.343493 }#
# " "= 1.467174#