Question

How do you find the area using the trapezoidal approximation method, given `sinpi*x dx`, on the interval [2, 5] with n=25?

Answer 1

Trapezium rule gives:

`int_2^5 \ sin(pix) \ dx ~~ 0.629062`

Explanation:

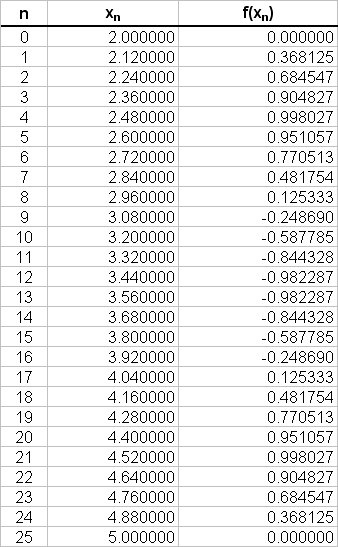
The values of `f(x)=sin(pix)` are tabulated as follows (using Excel) working to 5dp

Using the trapezoidal rule:

`int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}`

We have:

`int_2^5 \ sin(pix) \ dx ~~ 0.119999/2 { (0 - 0.000001) + 2(0.368124`
`" "+ 0.684547 + 0.904827 + 0.998026 + 0.951056 + 0.770513`
`" "+ 0.481753 + 0.125333 - 0.24869 - 0.587786 - 0.844328`
`" "- 0.982288 - 0.982288 - 0.844328 - 0.587786 - 0.24869`
`" " + 0.125333 + 0.481753 + 0.770513 + 0.951056 + 0.998026`
`" "+ 0.904827 + 0.684547 + 0.368124) }`

`" "=0.059999 { - 0.000001 + 2(5.242183) }`
`" "=0.059999 { - 0.000001 + 10.484367 }`
`" "=0.059999 { + 10.484367 }`
`" "=0.629062`

Let's compare this to the exact value:

`int_2^5 \ sin(pix) \ dx = [-cos(pix)/pi]_2^5`
`" " = (-1/pi)[cos(pix)]_2^5`
`" " = (-1/pi)(cos(5pi)-cos(2pi))`
`" " = (-1/pi)(-1-1)`
`" " = 2/pi`
`" " ~~ 0.6366197724 ...`