Question

How do you find the area using the trapezoidal approximation method, given `sinx(dx)`, on the interval [0, pi] with n=10?

Answer 1

The answer `A=113.652`

Explanation:

Follow the steps below
-Firstly:[sketch the function f(x)=sin(x) on interval `[0,pi]`

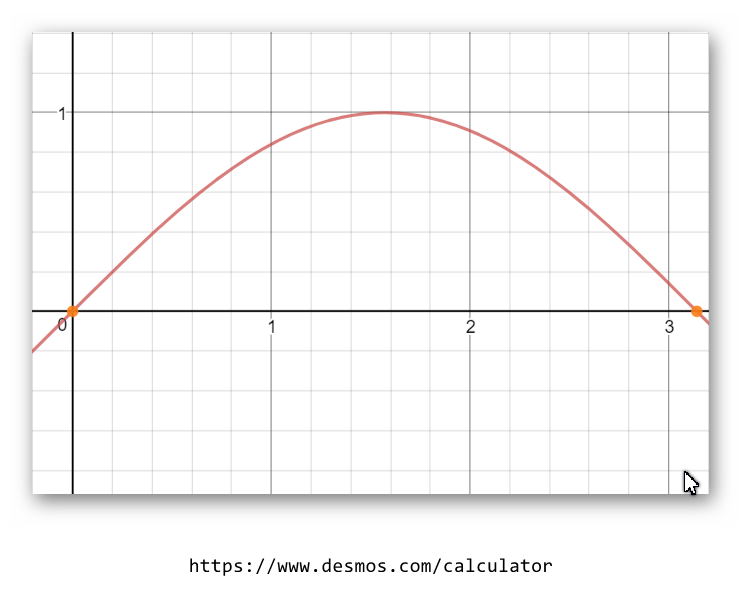
-secondly:[find the width=(b-a)/n ]

`width=(b-a)/n=(pi-0)/10=pi/10`

-Thirdly: write the parts of interval

`[0,pi/10] [pi/10,2pi/10] [2pi/10,3pi/10] [3pi/10,4pi/10]`

`[4pi/10,5pi/10] ........[9pi/10,pi]`

the sketch of function after separate it by intervals

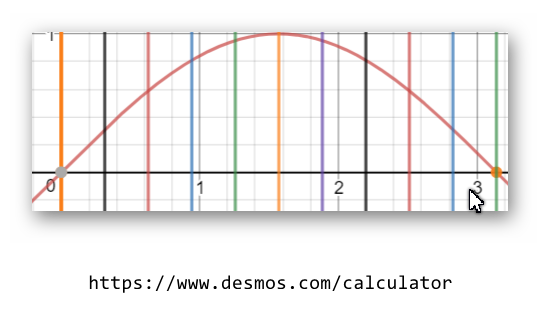
-Fourthly calculate the area by using the law:

`A=(b-a)/(2n)[f(x_0)+2f(x_1)+2f(x_2)+........+2f(x_(n-1))+f(x_n)]`

`A=pi/20[f(0)+2f(pi/10)+2f(2pi/10)+2f(3pi/10)+2f(4pi/10)+2f(5pi/10)+2f(6pi/10)+2f(7pi/10)+2f(8pi/10)+2f(9pi/10)+f(pi)]`

`pi/20[0+0.618+1.176+1.618+1.902+2+1.902+1.618+1.176+0.618+0]`

`A=pi/20(12.628)=9*(12.628)=113.652`

Note `pi=180`