How do you find the area using the trapezoidal approximation method, given #sqrtx#, on the interval [1,4] with n=3?
1 Answer
# int_1^4 sqrt(x) \ dx = 4.646 # (4dp)
(For comparison the exact value is
Explanation:
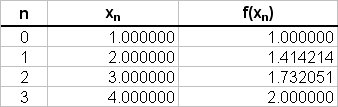
The values of
The Trapezium Rule:
# int_a^bydx ~~ h/2{(y_0+y_n)+2(y_1+y_2+...+y_(n-1))}#
uses a series of two consecutive ordinates and a best fit straight line to form trapeziums to approximate the area under a curve, It will have 100% accuracy if
So,
# int_1^4 sqrt(x) \ dx = 1/2 { (1 + 2) + 2(1.414213 + 1.73205) } #
# " "= 0.5 { + 3 + 2(3.146264) } #
# " "= 0.5 { + 3 + 6.292528 } #
# " "= 0.5 { + 9.292528 } #
# " "= 4.646264 #
Exact Value:
# int_1^4 sqrt(x) \ dx = [2/3x^(3/2)]_1^4 #
# " "=2/3{4^(3/2)-1^(3/2)} #
# " "= 2/3(8-1) #
# " "= 14/3#
# " "= 4.6666dot6#