How do you find the area using the trapezoidal approximation method, given #(x²-6x+9) dx#, on the interval [0,3] with n=3?
1 Answer
Oct 29, 2017
# int_0^3 \ x^2-6x+9 \ dx ~~ 9.5 #
Explanation:
We have:
# y = x^2-6x+9 #
We want to estimate
# Deltax = (3-0)/3 = 1#
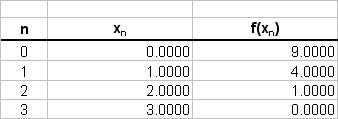
Note that we have a fixed interval (strictly speaking a Riemann sum can have a varying sized partition width). The values of the function are tabulated as follows;
Trapezium Rule
# A = int_0^3 \ x^2-6x+9 \ dx #
# \ \ \ ~~ 1/2 * { 9 - 0 + 2*(4 + 1) } #
# \ \ \ = 0.5 * { 9 + 2*(5) } #
# \ \ \ = 0.5 * { 9 + 10 } #
# \ \ \ = 0.5 * 19 #
# \ \ \ = 9.5 #
Actual Value
For comparison of accuracy:
# \ \ \ = [x^3/3-3x^2+9x]_0^3 #
# \ \ \ = 9-27+27 #
# \ \ \ = 9 #