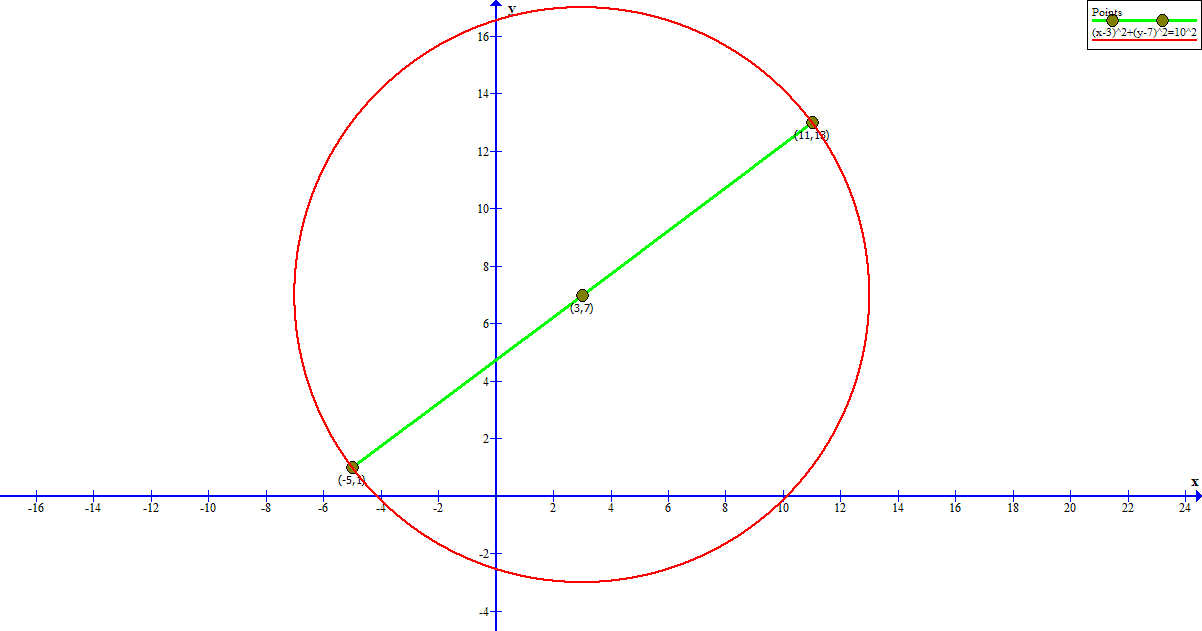
If #(-5,1)# and #(11,13)# are diameter endpoints then the center of the circle is at the midpoint between them:
Center at #((-5+11)/2,(1+13)/2)=(color(blue)3,color(red)7)#
The radius is the distance from the center, #(3,7)# to a diameter endpoint (I will use #(11,13)# but either should work).
By Pythagorean Theorem
Radius #= sqrt((11-3)^2+(13-7)^2)#
#color(white)("XXX")=sqrt(8^2+6^2)#
#color(white)("XXX")=sqrt(64+36)#
#color(white)("XXX")=sqrt(100)#
#color(white)("XXX")=color(green)(10)#
The center-radius form for a s circle with center at #(color(blue)a,color(red)b)# and radius #color(green)r# is
#color(white)("XXX")(x-color(blue)a)^2+(y-color(red)b)^2=color(green)r^2#
Using the derived values
#color(white)("XXX")(x-color(blue)3)^2+(y-color(red)7)^2=color(green)10^2#
Here's a graph of #(x-3)^2+(y-7)^2=10^2# for verification purposes: