Question

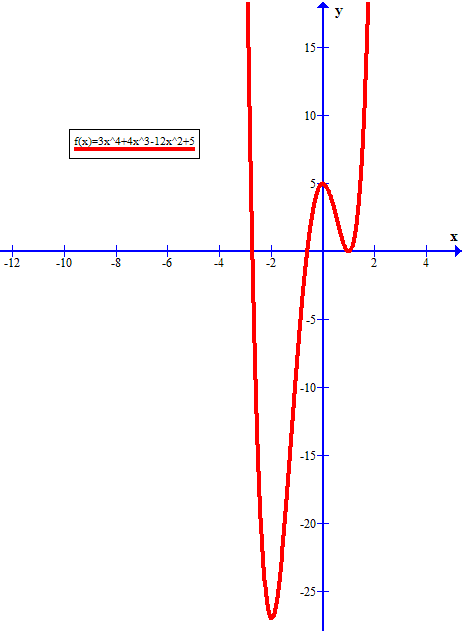
How do you find the critical numbers for `f(x) = 3x^4 + 4x^3 - 12x^2 + 5` to determine the maximum and minimum?

Answer 1

Critical points occur at `x in {-2,0,1}`

Explanation:

Critical point occur where the derivative of the function is equal to zero.

Given
`color(white)("XXX")f(x)=3x^4+4x^3-12x^2+5`

First derivative:
`color(white)("XXX")f'(x)=12x^3+12x^2-24x`
which can be factored as
`color(white)("XXX")=(12)(x)(x^2+1-2)`

`color(white)("XXX")=(12)(x)(x+2)(x-1)`

Which implies the critical points (when `f'(x)=0`) occur when
`color(white)("XXX")x=0`
`color(white)("XXX")(x+2)=0color(white)("xxx")rarr x=-2` and
`color(white)("XXX")(x-1)=0color(white)("xxx")rarr x=+1`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

While not explicitly asked for in this question,
you can determine if each of these critical points is a minimum or maximum by evaluating the second derivative at each critical value.
Results greater than zero indicate a local minimum;
results less than zero indicate a local maximum;
results equal to zero indicate an inflection point.

#{: (f''(x),=36x+24x-24,,), ("at "x=-2,= +72,>0,"minimum"),("at "x=0,=-24, <0, "maximum"),("at "x=+1,=+36,>0,"maximum") :}#

Here is the graph for verification: