Question

How do you find the critical numbers of `f(x)= 2x^3 + 3x^2-12x`?

Answer 1

So the critical points are `(-1,20)` and `(1,-7)`

`(-1,20)` is a maximum
`(1,-7)` is a minium

Explanation:

We have `f(x) = 2x^3 + 3x^2 - 12x`

To identify the critical vales, we differentiate and find find values of `x` st `f'(x)=0`

# { ( f'(x) < 0, => f(x) " is decreasing" ), ( f'(x) = 0, => f(x) " is stationary" ), ( f'(x) > 0, => f(x) " is increasing" ) :} #

Differentiating wrt `x`' we have:

`f'(x) = 6x^2 + 6x - 12` .... [1]

At a critical point, `f'(x)=0`

`f'(x)=0 => 6x^2 + 6x - 12 = 0`
`:. x^2 + x - 2 = 0`
`:. (x+2)(x-1) = 0`
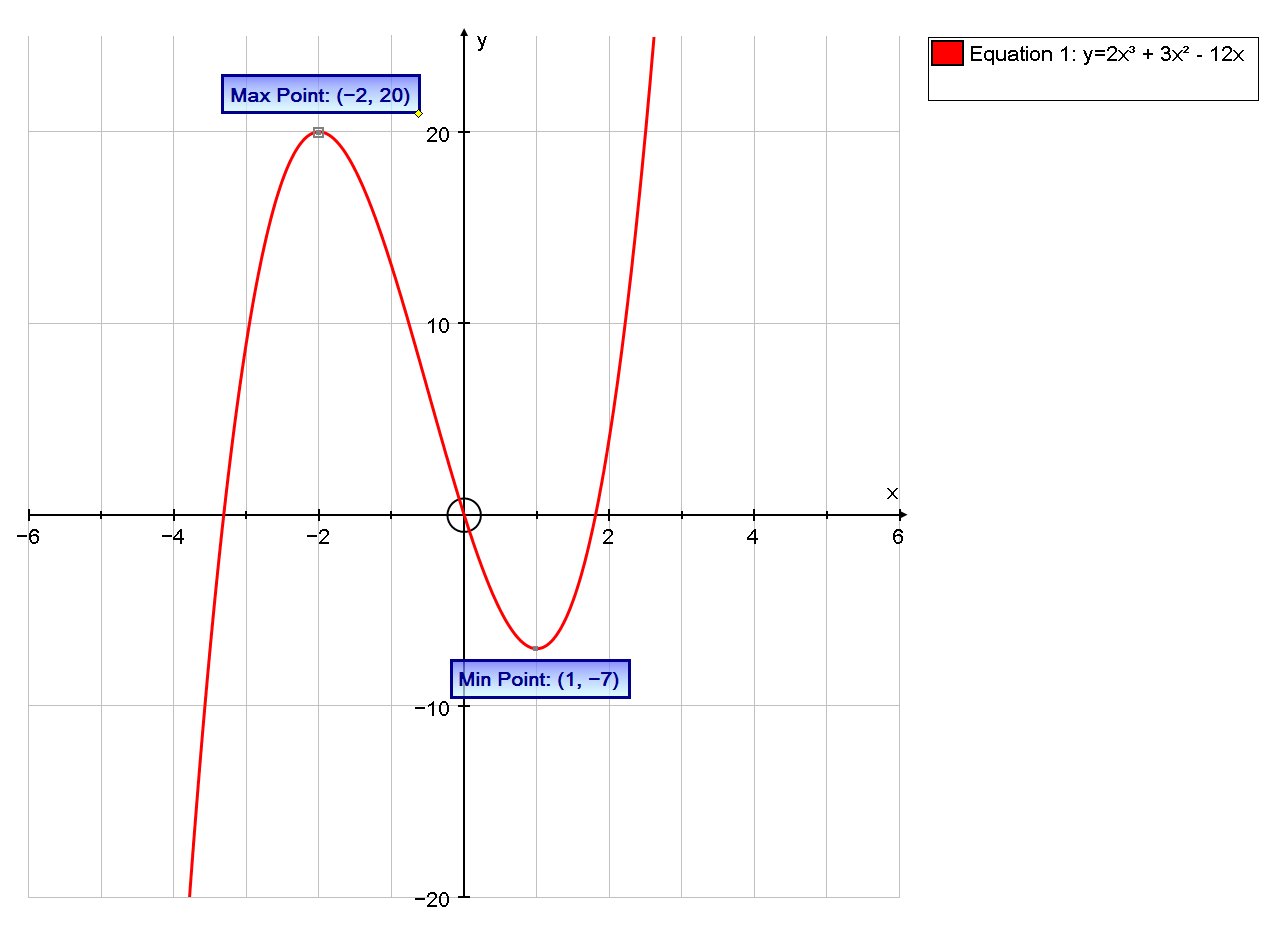
`x=-2,1`

Ton find the y-coordinate we substitute the required value into `f(x)`
`x=-2 => f(-2)=2(-8)+3(4)-12(-2) = -16+12+24=20`
`x=1 => f(1)=2+3-12=-7`

So the critical points are `(-1,20)` and `(1,-7)`

Although this answers the question, let's go a bit further and identify the nature of these critical points by looking at the sign of second derivative, and

# { ( f''(x) < 0, => f'(x) " is decreasing" => "maximum" ), ( f''(x) = 0, => f'(x) " is stationary" => "inflection" ), ( f''(x) > 0, => f'(x) " is increasing" => "minimum" ) :} #

Differentiating [1] wrt `x` gives s;

`f''(x) = 12x + 6`
`x=-2 => f''(-2)=-14+6 < 0`, ie a maximum
`x=1 => f''(1)= 12+6>0`, ie a minimum

Incidental, As this is a cubic with a positive coefficient of `x^3`, we can deduce that the critical point corresponding to the smallest value of `x` must be the maximum and that corresponding to the larger value must be the maximum. It is not possible to have any other possibility!