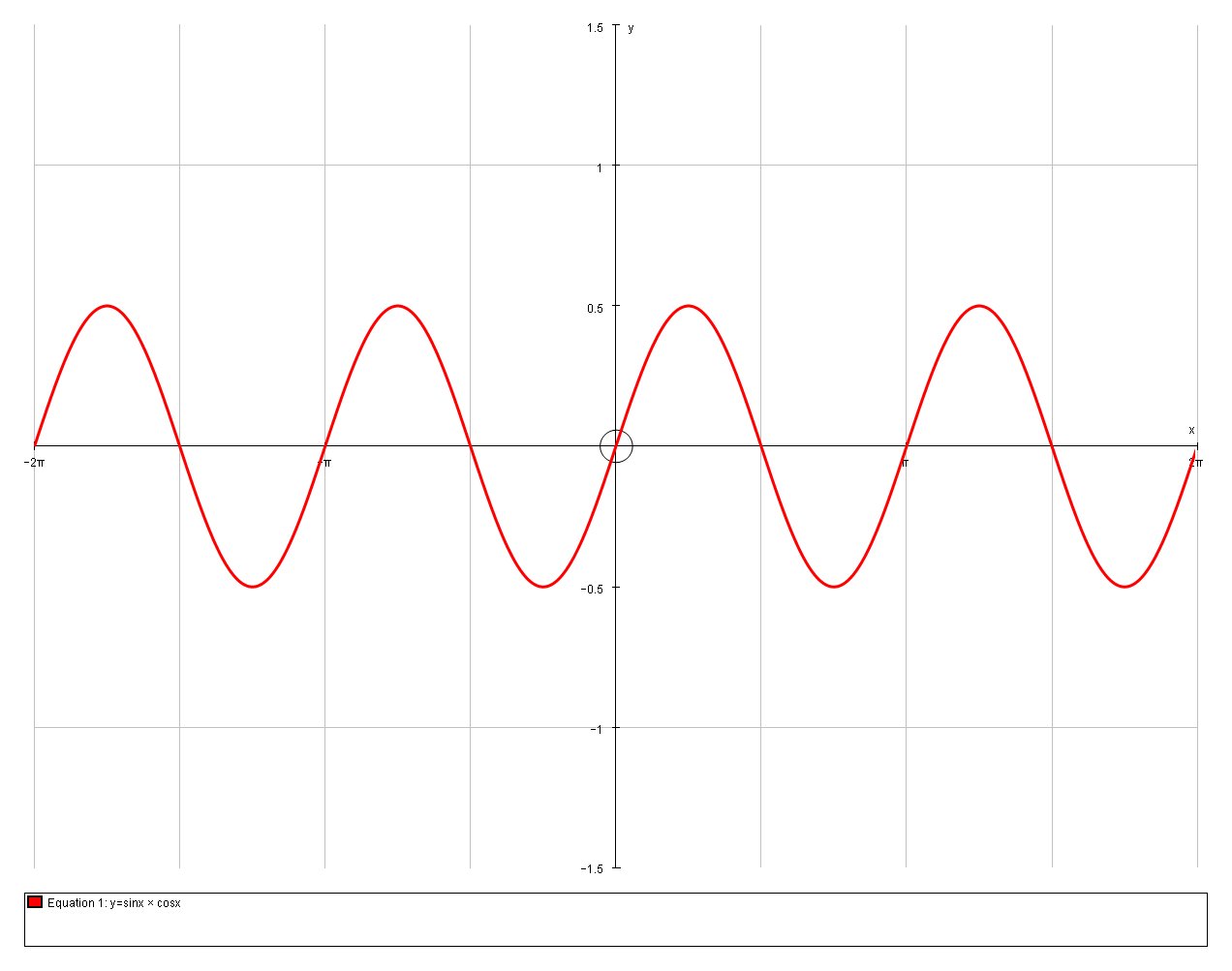
How do you find the critical numbers of #f(x)=sinxcosx#?
1 Answer
Feb 1, 2017
Critical numbers of
# x \ \ = pi/4 + (npi)/2 \ \ \ \ n in ZZ#
eg#x = +-pi/4, +-3pi/4, +-5pi/4, ... #
Explanation:
We have:
# f(x) = sinx cos x #
Differentiating wrt
# f'(x) = (sinx) (-sinx) + (cosx) (cosx) #
# " "= cos^2x -sin^2x #
# " "= cos(2x) #
At a critical point
# :. cos (2x) = 0 #
# :. 2x = pi/2 + npi #
# :. x \ \ = pi/4 + (npi)/2 \ \ \ \ n in ZZ#
Hence critical numbers of
# x \ \ = pi/4 + (npi)/2 \ \ \ \ n in ZZ#
eg#x = +-pi/4, +-3pi/4, +-5pi/4, ... #
We can see these values of