How do you find the critical points to sketch the graph #h(x)=27x-x^3#?
1 Answer
Critical Points are:
Graph of
Explanation:
Given:
We need to find the Critical Points
Definition of Critical Points:
Let
We call
(1)
(2)
Also not that,
(3) the derivative gives us the slope of the tangent line
(4) the Critical Points are points where the slope of the tangent line is ZERO
Given:
We will find the derivative first.
We are differentiating a polynomial. Hence, it is easy.
Note that
We will set this derivative equal to ZERO, to find our Critical Points.
Subtract
Divide both sides by
Divide both sides by 3
Taking Square Root on both sides
Hence our Critical Points are
Please analyze the graph below:
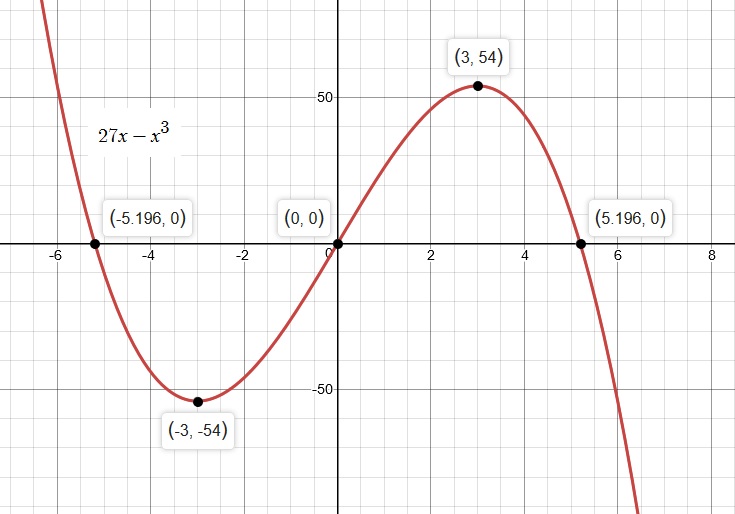
Please observe the following on the graph:
At the Critical Points, tangent lines are horizontal in this example

