How do you find the definite integral of cos^4(2x)sin(2x) dx?
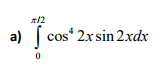
Please help guide me through this question with steps. I just want to know how to approach this question. I tried using u-substitution with u = 2x but I am unable to find the answer. Thanks for your time.
Please help guide me through this question with steps. I just want to know how to approach this question. I tried using u-substitution with u = 2x but I am unable to find the answer. Thanks for your time.
1 Answer
Dec 17, 2017
Explanation:
Remember that the point of u-substitutions is to eliminate complex polynomials or functions. Under this mentality it would make sense that we try to eliminate the trigonometric functions sine and cosine. We will let
Notice how the
which yields

