How do you find the distance between #O(-2, 10)# and #P(-8,3)#?
3 Answers
Explanation:
#" find the distance (d) using the "color(blue)"distance formula"#
#color(red)(bar(ul(|color(white)(2/2)color(black)(d=sqrt((x_2-x_1)^2+(y_2-y_1)^2))color(white)(2/2)|)))#
#"let "(x_1,y_1)=(-2,10)" and "(x_2,y_2)=(-8,3)#
#d=sqrt((-8-(-2))^2+(3-10)^2)#
#color(white)(d)=sqrt(36+49)=sqrt85~~9.22#
distance
Explanation:
distance
distance
distance
distance
I hope that helps :)
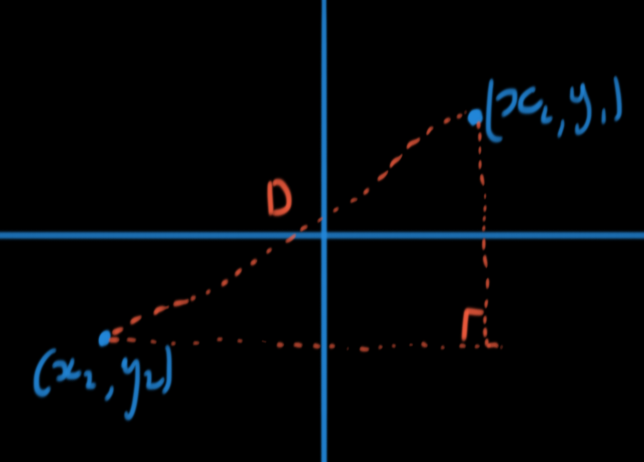
Giving an understanding to the distance formula...
Explanation:
Explanation to prior answer.
The '
Let there be two different points
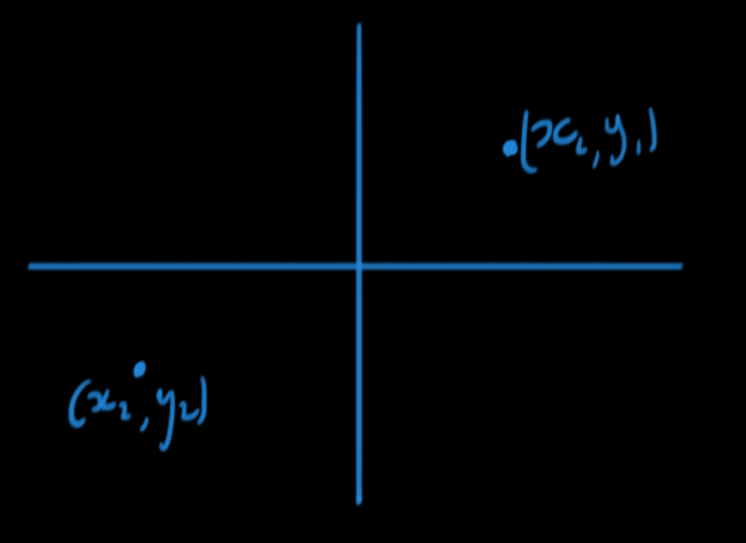
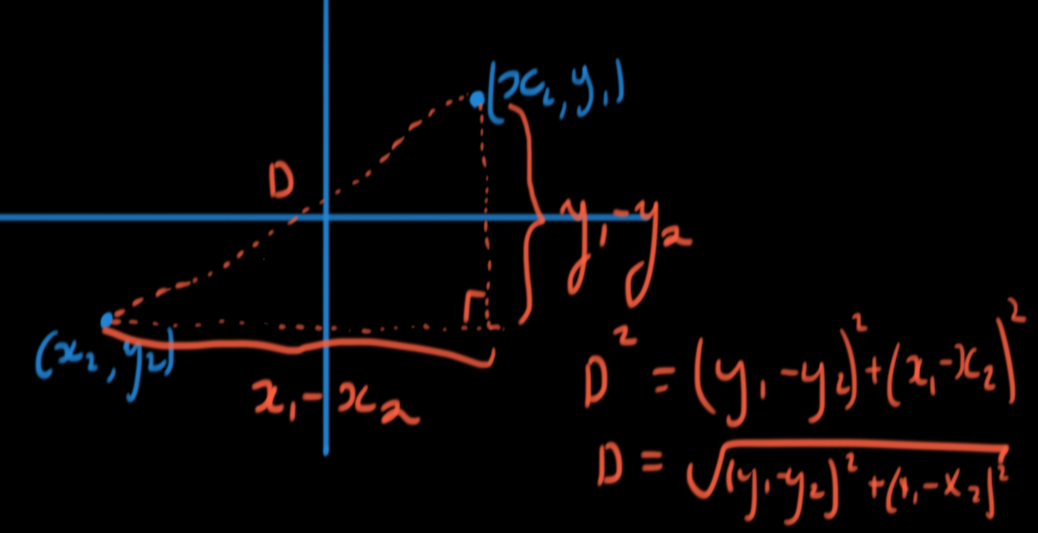
Now drawring dotted lines... We see this is a right angled trianlge, were we can use pythagerouses theorem...