How do you find the domain and range of a function in interval notation?
1 Answer
There are so many different kinds of functions, but domain and range are important parts of your study of functions.
Let me give you some examples of polynomial functions:
y = 3x + 1, y =
All polynomials have a domain of "All Real Numbers". In interval notation, we write:
Polynomials with ODD degree (highest power of x) stretch their way from low to high through all real numbers in the vertical direction. This means that their Range is "All Real Numbers" again:
Polynomials with EVEN degree must have either a maximum or minimum value. If the graph has a minimum value, then its y-values (Range) stretch from that number, up to 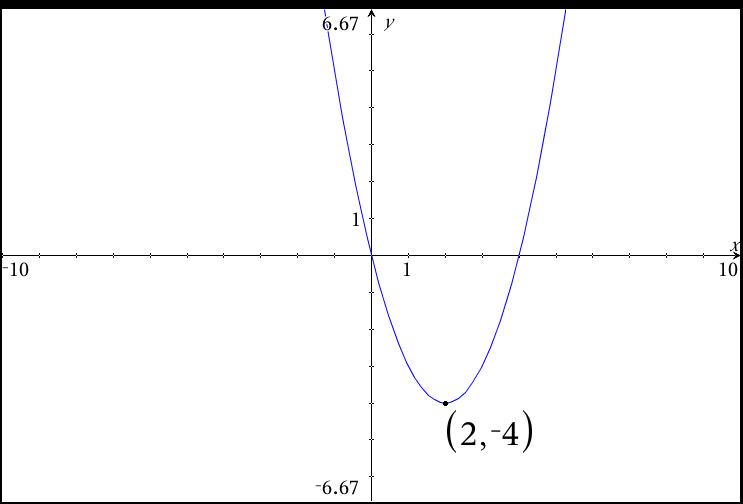
Notice that whenever we use the
Your study of domain and range has just begun, and will include a wide variety of functions besides polynomials. When you discover a new function that behaves differently, carefully analyze its input and output values. You are on the way to great things!

