Question

How do you find the domain and range of `x+3 =0`?

Answer 1

`color(red)(x+3=0)` is an equation
It is not a function.
The terms "domain" and "range" only apply to functions.

Explanation:

Possibility 1: You really wanted the solution
`color(white)("XXX")x=-3`

Possibility 2: You wanted the domain and range of `f(x)=x+3`
`color(white)("XXX")`Domain: `x in RR (or CC)color(white)("xxxx)`all possible values of `x` are valid
`color(white)("XXX")`Range: `f(x) in RR (or CC)color(white)("xxx")`any value can be generated using a suitable value for `x`

Possibility 3: This was a trick question if see if you knew that the terms do not apply to equations

Answer 2

domain: `(-3)`
range: `(-oo,oo)`

Explanation:

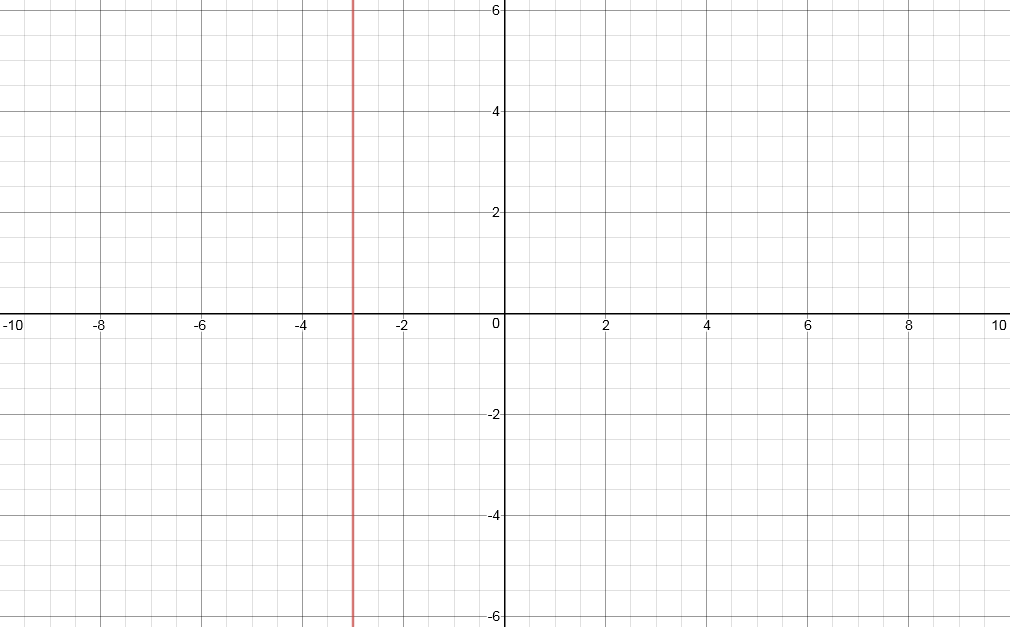
domain: the range of values `x` could take

`x+3=0`
`x=0-3 = -3`

here, `x` can only take one value, so the domain is `(-3)`

range: the range of values `y` could take:

since the only condition for the line is that `x=0`, `y` could take any real value,
so the range is `(-oo,oo)`