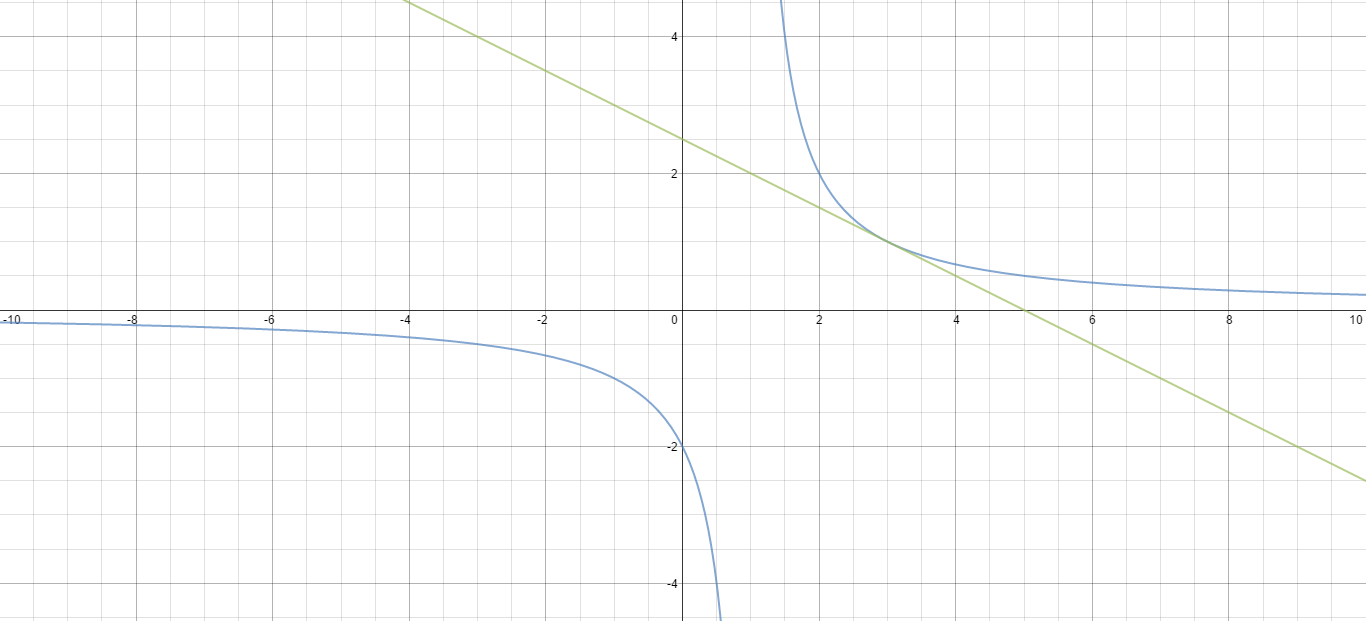
How do you find the equation of the line tangent to #f(x)= 2/(x-1)# at x=3?
1 Answer
Explanation:
To find the equation of the line tangent to the given function, you will need to:
#1# . Find the derivative.
#2# . Substitute#x=3# into the given function to find the y-coordinate
#3# . Substitute#x=3# into the derivative to find the slope of the tangent.
#4# . With the acquired data, use the slope formula to determine the equation of the tangent.
Finding The Derivative
In your case, to find the derivative, you will need to use four rules - the constant multiple rule, the reciprocal rule, the difference rule, and the power rule. The rules can be expressed as follows:
#color(red)("Constant Multiple Rule")# :#[cf(x)]'=c[f(x)]'#
#color(green)("Reciprocal Rule")# :#[1/f(x)]'=-(f'(x))/[f(x)]^2#
#color(blue)("Difference Rule")# :#[f(x)-g(x)]'=f'(x)-g'(x)#
#color(purple)("Power Rule")# :#(x^n)'=nx^(n-1)#
#f(x)=2/(x-1)#
#f'(x)=2[1/(x-1)]#
#f'(x)=-2[((x-1)')/(x-1)^2]#
#f'(x)=-2[((1-0))/(x-1)^2]#
#f'(x)=-2[1/(x-1)^2]#
#f'(x)=-2/(x-1)^2#
Finding the Coordinates of the Point
To find the y-coordinate of the point when
#f(x)=2/(x-1)#
#f(3)=2/(3-1)#
#f(3)=1#
Finding the Slope of the Tangent
To find the slope of the equation tangent to the point
#f'(x)=-2/(x-1)^2#
#f'(3)=-2/(3-1)^2#
#f'(3)=-2/4#
#f'(3)=-1/2#
Finding the Equation of the Tangent
Using the equation of a line in point-slope form, substitute your known values into the equation. Then rewrite the equation in slope-intercept form:
#y-y_1=m(x-x_1)#
#y-1=-1/2(x-3)#
#y-1=-1/2x+3/2#
#y=-1/2x+5/2#
If you graph the given function and the tangent, you will see that the line intersects