Question

How do you find the equation of the line tangent to the graph of `f(x) = x^2 + 5x` at x = 4?

Answer 1

We need a point on the line and the slope of the line.

Explanation:

At `x=4`, the point on the graph of `f(x) = x^2 + 5x` has `y` coordinate `f(4) = (4)^2+5(4) = 36`.

So we know that the point `(4, 36)` is on the line we are looking for.

There are several good ways to present this material to students and I can't know which one you are seeing.

My guess is that you've been given one of the following as the definition and the other as an equivalent:

The slope of the tangent line to the graph of function `f` at `x=a` is:

`lim_(xrarra)(f(x)-f(a))/(x-a)` Provided that the limit exists.

OR

`lim_(hrarr0)(f(a+h)-f(a))/h` Provided that the limit exists.

end of definition

Given a choice, let's use the second (the algebra that way seems simpler to many students)

In this question:

`f(x) = x^2+5x` and `a = 4`, so the slope of the tangent line is:

`lim_(hrarr0)(f(4+h)-f(4))/h = lim_(hrarr0) (overbrace(((4+h)^2+5(4+h)))^f(4+h) - overbrace(((4)^2+5(4)))^f(4))/h`

`= lim_(hrarr0)(16+8h+h^2+20+5h-(16+20))/h`

`= lim_(hrarr0)(8h+h^2+5h)/h`

`= lim_(hrarr0)(13h+h^2)/h`

Now, let's take a moment to observe that if we tried to evaluate the limit by substitutiong `0` for `h` in any of the lines, we would get the indeterminate form `0/0`.
But now we have reached a point where we can reduce the fraction to eliminate that pesky `h` in the denominator:

`= lim_(hrarr0)(cancel(h)(13+h))/cancel(h)`

For every `h` other than `0`, the thing we are interested in: `(f(4+h)-f(4))/h` is equal to `13+h`.
When `h=0` the first thing is not a number at all. So we can not make `h=0` in the first expression.
But the limit as `hrarr0` doesn't care what happens at 0, just what happens close to `0`.

So, we have:

`lim_(hrarr0)(f(4+h)-f(4))/h = lim_(hrarr0)(13+h) = 13`

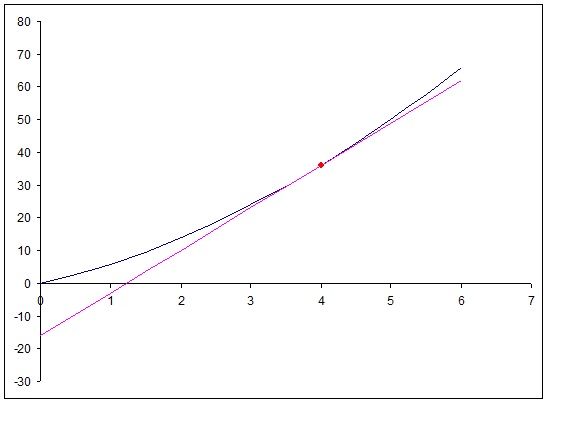
The slope of the line tangent to the graph at `x= 4` is 13.

And the point `4,36)` is on that line, so the equation of the line is:

`y-36 = 13(x-4)" "` which can be put in slope-intercept form:

`y = 13x-16`

Final note
Soon, you will learn more general results that will let you find the slope of the tangent line much, much more quickly. But it is important to understand this idea of the limit.

Answer 2

I found: `y=13x-16`

Explanation:

First we find the slope `m` of the tangent by evaluating the derivarive of the function at `x=4`:
`f'(x)=2x+5`
and: `f'(4)=8+5=13` which is the slope of the tangent.
We find the coordinate `y` of the tangence point by sbstituting `x=4` into the original function so:
`y=f(4)=16+20=36`
So we need the equation of a line with slope `m=13` and passing through `x_0=4, y_0=36`; we can use the relationship:
`y-y_0=m(x-x_0)`
`y-36=13(x-4)`
`y=13x-16`

Graphically: