Question

How do you find the equation of the line tangent to the graph of `y= 1/ (1+x^2)` at the point (2, 0.2)?

Answer 1

I found: `y=-4/25x+13/25`

Explanation:

I would start by fnding the slope of the tangent evaluating the derivative of the function at `x=2`:
`y'=(-2x)/(1+x^2)^2`
at `x=2`
`y'(2)=-4/(5^2)=-4/25` which is the slope `m` of the tangent.
So the equation can be found using:
`y-y_0=m(x-x_0)`
`y-0.2=-4/25(x-2)`
`y-2/10=-4/25(x-2)`
`y-1/5=-4/25(x-2)`
`y=1/5-4/25x+8/25`
`y=-4/25x+13/25`

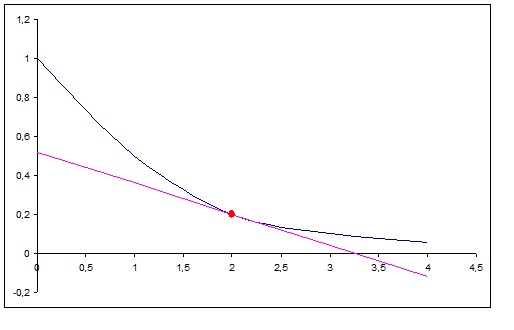
Graphically: