Question

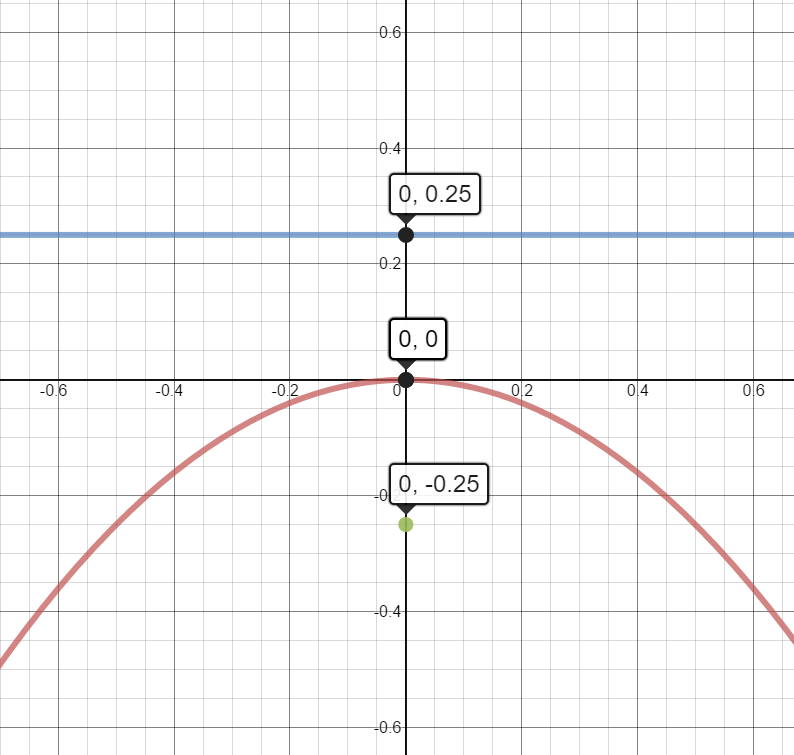
How do you find the equation of the parabola whose Focus (0,-1/4) and directrix (0,1/4)?

Answer 1

The vertex will lie halfway between the focus and directrix.

Explanation:

I think you meant to write that the directrix is `y=1/4`. Assuming that is true, then the directrix lies above the focus, so this parabola opens downward (concave down).

Vertex `=(0,0)` which is halfway between the focus and directrix.

Distance between focus and vertex `p= 1/4`

Coefficient `abs(a)=1/(4xx1/4)=1`

The sign on `a` is negative , so `a=-1`

Equation of parabola : `y=-x^2`

hope that helps!