Question

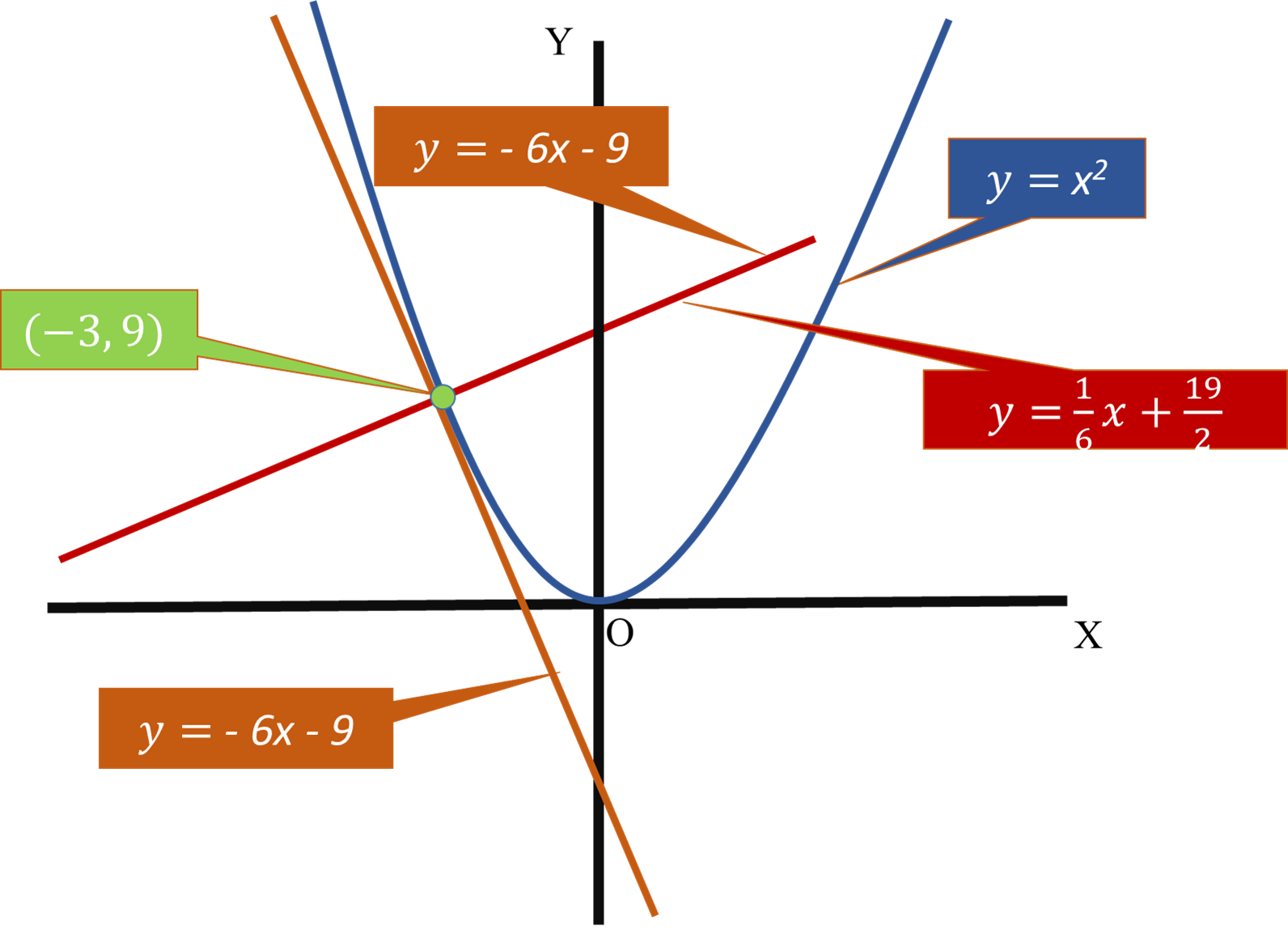
How do you find the equation of the tangent and normal line to the curve `y=x^2` at x=-3?

Answer 1

Equation of the tangent

`y=-6x-9`

Equation of the Normal

`y=1/6x+19/2`

Explanation:

Given -

`y=x^2`

It is a quadratic function. The curve is a upward facing parabola.

Its first derivative gives the slope at any given point on the curve.

`dy/dx=2x`

Slope exactly at `x=-3`

`m_1=2(-3)=-6`

At `x=-3 ; y=(-3)^2=9`

The tangent and Normal are passing through the point `(-3, 9)`

Slope of the tangent is `m_2=-6`

Steps to get Equation of the tangent -

`mx+c=y`

`(-6)(-3)+c=9`

`18+c=9`

`c=9-18=-9`

Equation of the tangent is -

`y=-6x-9`

Steps to get Equation of the Normal -

Normal's slope `m_3=-(1/(m_2))=-(1/(-6))=1/6`

`mx+c=y`
`1/6(-3)+c=9`
`-1/2+c=9`
`c=9+1/2=(18+1)/2=19/2`

Equation of the Normal -

`y=1/6x+19/2`