Question

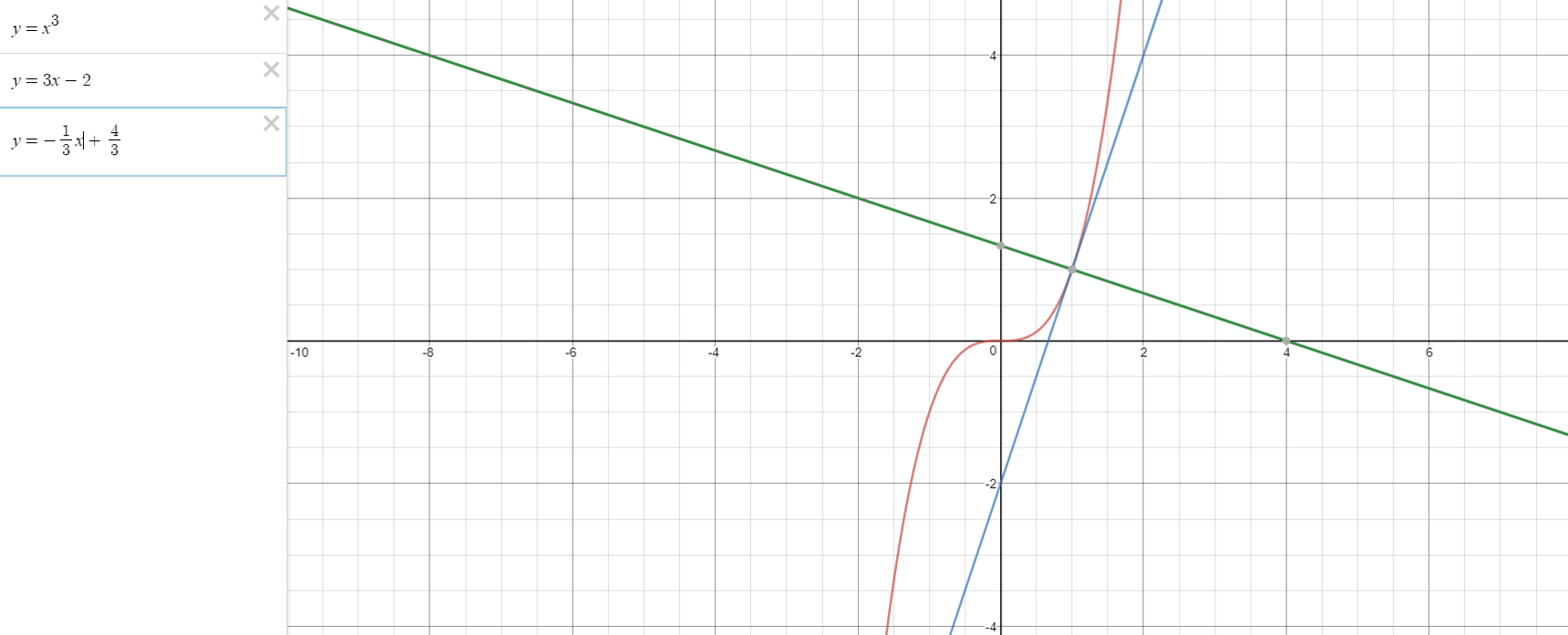
How do you find the equation of the tangent and normal line to the curve `y=x^3` at x=1?

Answer 1

The equation of the tangent `y=3x-2`
Then the equation of the normal is `y=-1/3x+4/3`

Explanation:

Given -

`y=x^3`

At `x=1; y= 1^3=1`

`(1,1)`
It is at this point there is a tangent and a normal.

The slope of the tangent is equal to the slope of the given curve at `x=1`

The slope of the curve at any given point is, its first derivative.

`dy/dx=3x^2`

Slope of the curve at `x=1`

`m=3xx1^1=3`

Then the slope of the tangent `m_1=3`

The equation of the tangent

`y-y_1=m_1(x-x_1)`
`y-1=3(x-1)`
`y-1=3x-3`
`y=3x-3+1`
`y=3x-2`

If the two lines cut vertically then `m_1 xx m_2=-1`

`m_2=(-1)/(m_1)=(-1)/3=-1/3`

Then the equation of the normal is -

`y-y_1=m_1(x-x_1)`

`y-1=-1/3(x-1)`
`y-1=-1/3x+1/3`
`y=-1/3x+1/3+1`
`y=-1/3x+4/3`