Question

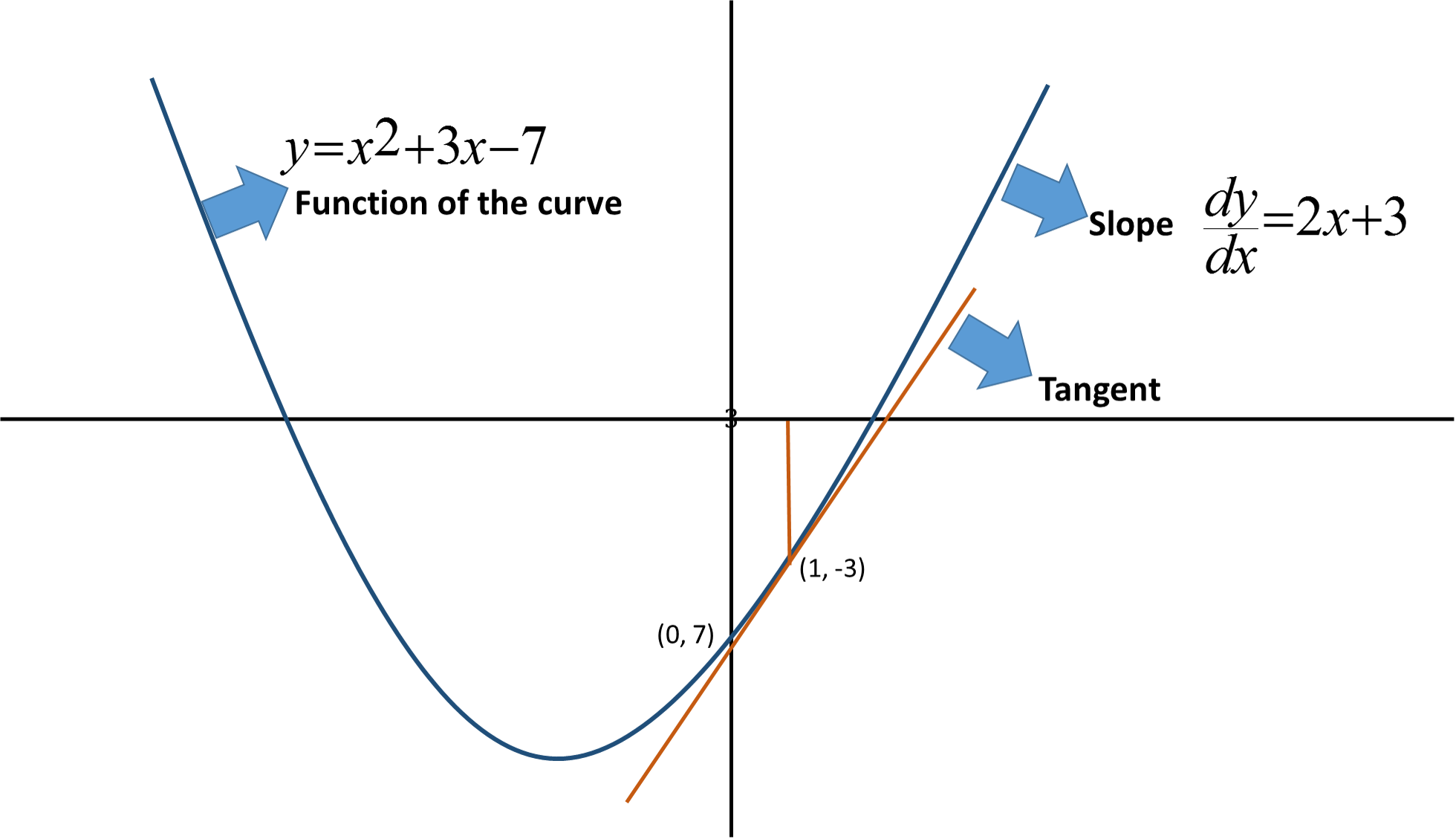
How do you find the equation of the tangent line to the graph of `f(x)=x^2+3x-7` at x =1?

Answer 1

y = 5x – 4

Explanation:

Remember this-

To find the equation of a straight line, we need two information –

They are (i) slope of the line and (ii) (x, y) co-ordinates of a point on that line.

Tangent is a straight line.

The given function is
y =`x^2 + 3x – 7`
It is a U shaped curve or parabola. It doesn’t have uniform slope throughout its length.

Its slope at any given point is its first derivative.

`dy/dx`= 2x + 3

At x = 1, its slope is `dy/dx` = 2(1) + 3 = 5

At x = 1 , the slope of the curve is 5.

A tangent is drawn to that point. To find the y co-ordinate of the point substitute x = 1 in the given function.

Y = 12 + 3(1) – 7 = -3

(1, -3) is a point on the tangent. The slope of the tangent is m = 5.
The equation of the tangent is

y – y1 = m(x – x1)
y – (- 3) = 5(x – 1)
y +3 = 5x – 1
y = 5x – 1 – 3

y = 5x – 4