Question

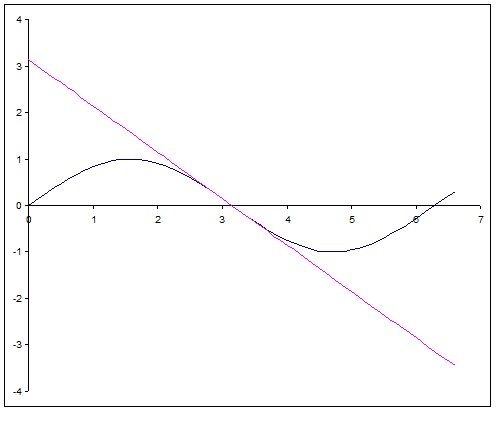
How do you find the equation of the tangent line to the graph of `y = sin(x)` at `x = pi`?

Answer 1

First evaluate the derivative of your function and evaluate it in your point with `x=pi` to find the slope of the tangent line:
`y'=cos(x)`
in `x=pi`
`y'(pi)=cos(pi)=-1`

Second find the point where your tangent touches your curve. You know that `x=pi` and substituting into your original function you'll get the corresponding value of y which is `y=sin(pi)=0`.
So, the tangent line has slope `m=-1` and passes through (`x_0=pi,y_0=0`);
the equation can be found using:
`y-y_0=m(x-x_0)`
or
`y-0=-1(x-pi)`
`y=-x+pi`

Graphically: