To find the equation of the tangent we need to find the gradient of the tangent so we need the derivative #dy/dx#
I will assume you know hoe differentiate implicitly and to apply the product rule. If not there are many examples to look through. I will do each part in a separate step so hopefully you can follow
We have: # x^2-2xy+4y^2=64 #
Differentiating wrt #x# we have
# d/dx(x^2) - d/dx(2xy) +d/dx(4y^2) = d/dx(64) #
The first and last term we can just deal with using straight forward rules to give:
# 2x - d/dx(2xy) +d/dx(4y^2) = 0 #
For the next term we apply the product rule to #(2x)(y)# give:
# 2x - {(2x)d/dx(y) + (y)d/dx(2x)} +d/dx(4y^2) = 0 #
# :. 2x - {(2x)dy/dx + (y)(2)} +d/dx(4y^2) = 0 #
# :. 2x - 2xdy/dx - 2y +d/dx(4y^2) = 0 #
And for the final term we need to differentiate implicit (by applying the chain rule) to give:
# 2x - 2xdy/dx - 2y +d/dy(4y^2)dy/dx = 0 #
# :. 2x - 2xdy/dx - 2y + 8ydy/dx = 0 #
# :. x - xdy/dx - y + 4ydy/dx = 0 #
We can now factorise #dy/dx# to get an explicit function for the derivative:
# dy/dx(4y-x) + x - y = 0 #
# :. dy/dx(4y-x) =y-x #
# :. dy/dx = (y-x)/(4y-x) #
We want the tangent when #x=2#
To get the coordinates on the curve where #x=2# we substitute #x=2# into the equation # x^2-2xy+4y^2=64 #:
# x=2 => 2^2-2(2)y+4y^2=64#
# :. 4-4y+4y^2=64#
# :. 4y^2-4y-60=0#
# :. y^2-y-15=0#
This does not factorise, so we can solve by completing the square (or using the quadratic formula):
# (y-1/2)^2-(1/2)^2-15 = 0 #
# (y-1/2)^2-1/4-15 = 0 #
# (y-1/2)^2-1/4-15 = 0 #
# (y-1/2)^2 = 61/4 #
# y-1/2 = +-sqrt61/2 #
# y = 1/2+-sqrt61/2 #
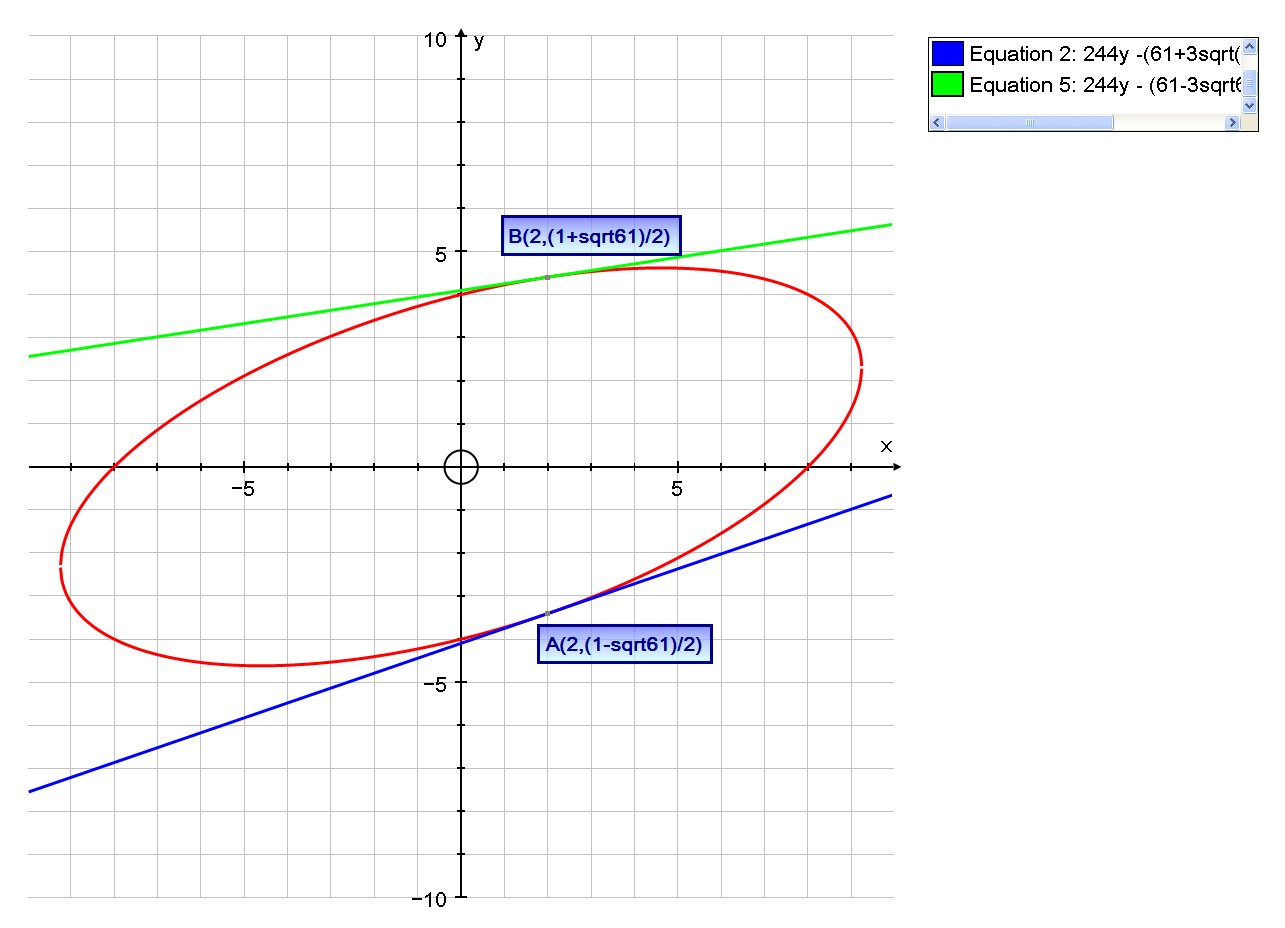
So the two points we are interested in are
# A(2,(1-sqrt61)/2) # and # B(2,(1+sqrt61)/2) #
Let us consider A first:
At # A(2,(1-sqrt61)/2) #,
# dy/dx = ((1-sqrt61)/2 - 2)/(4(1-sqrt61)/2-2) #
# :. dy/dx = ((1-sqrt61)/2 - 2)/(2-2sqrt61-2) #
# :. dy/dx = ((-3-sqrt61)/2)/(-2sqrt61) #
# :. dy/dx = (3+sqrt61)/(4sqrt61) #
# :. dy/dx = (3+sqrt61)/(4sqrt61) * (sqrt61)/(sqrt61)#
# :. dy/dx = (3sqrt61+61)/(4*61)#
# :. dy/dx = (61+3sqrt61)/244#
So the tangent has equation
# y - (1-sqrt61)/2 = (61+3sqrt61)/244 (x - 2) #
# :. 244y - 122(1-sqrt61) = (61+3sqrt61) (x - 2) #
# :. 244y -122+122sqrt(61) = 61x-122+3sqrt(61)x-6sqrt61 #
# :. 244y -(61+3sqrt(61))x +128sqrt(61) = 0 #
And at # B(2,(1+sqrt61)/2) #
# dy/dx = ((1+sqrt61)/2-2)/(4(1+sqrt61)/2-2) #
# :. dy/dx = ((1+sqrt61)/2-2)/(2+2sqrt61-2) #
# :. dy/dx = ((-3+sqrt61)/2)/(2sqrt61) #
# :. dy/dx = (-3+sqrt61)/(4sqrt61) #
# :. dy/dx = (-3+sqrt61)/(4sqrt61) * sqrt61/sqrt61#
# :. dy/dx = (-3sqrt61+61)/(4*61)#
# :. dy/dx = (61-3sqrt61)/244#
So the tangent has equation
# y - (1+sqrt61)/2 = (61-3sqrt61)/244(x-2) #
# :. 244y - 122(1+sqrt61) = (61-3sqrt61)(x-2) #
# :. 244y - 122 - 122sqrt61 = 61x-122 -3sqrt61x+6sqrt61 #
# :. 244y - (61-3sqrt61)x-128sqrt61 = 0#