How do you find the equations of both lines through point (2,-3) that are tangent to the parabola #y=x^2+x#?
2 Answers
The equations of the tangents that pass through
Explanation:
The gradient of the tangent to a curve at any particular point is given by the derivative of the curve at that point. So for our curve (the parabola) we have
# y=x^2+x #
Differentiating wrt
# dy/dx=2x+1 #
Let
# m = 2alpha + 1 \ \ \ # (using the derivative)
And as P lies on the curve we also have:
# beta = alpha^2+alpha \ \ \ # (using the curve equation)
And so the tangent at
#y - (alpha^2+alpha) = (2alpha+1)(x-alpha)#
if this tangent also passes through
# \ \-3 - (alpha^2+alpha) = (2alpha+1)(2-alpha)#
# :. -3 - alpha^2-alpha = 3alpha-2alpha^2+2#
# :. alpha^2 -4alpha-5=0#
# :. (alpha-5)(alpha+1)=0#
# :. alpha =-1,5#
If
#y - 0 = (-1)(x+1)#
# :. \ \ y=-x-1 #
If
# \ \ \ \ \ y - 30 = (11)(x-5)#
# :. y - 30 = 11x-55#
# :. \ \ \ \ \ \ \ \ \y = 11x-25#
Hence the equations of the tangents that pass through
We can confirm this graphically:
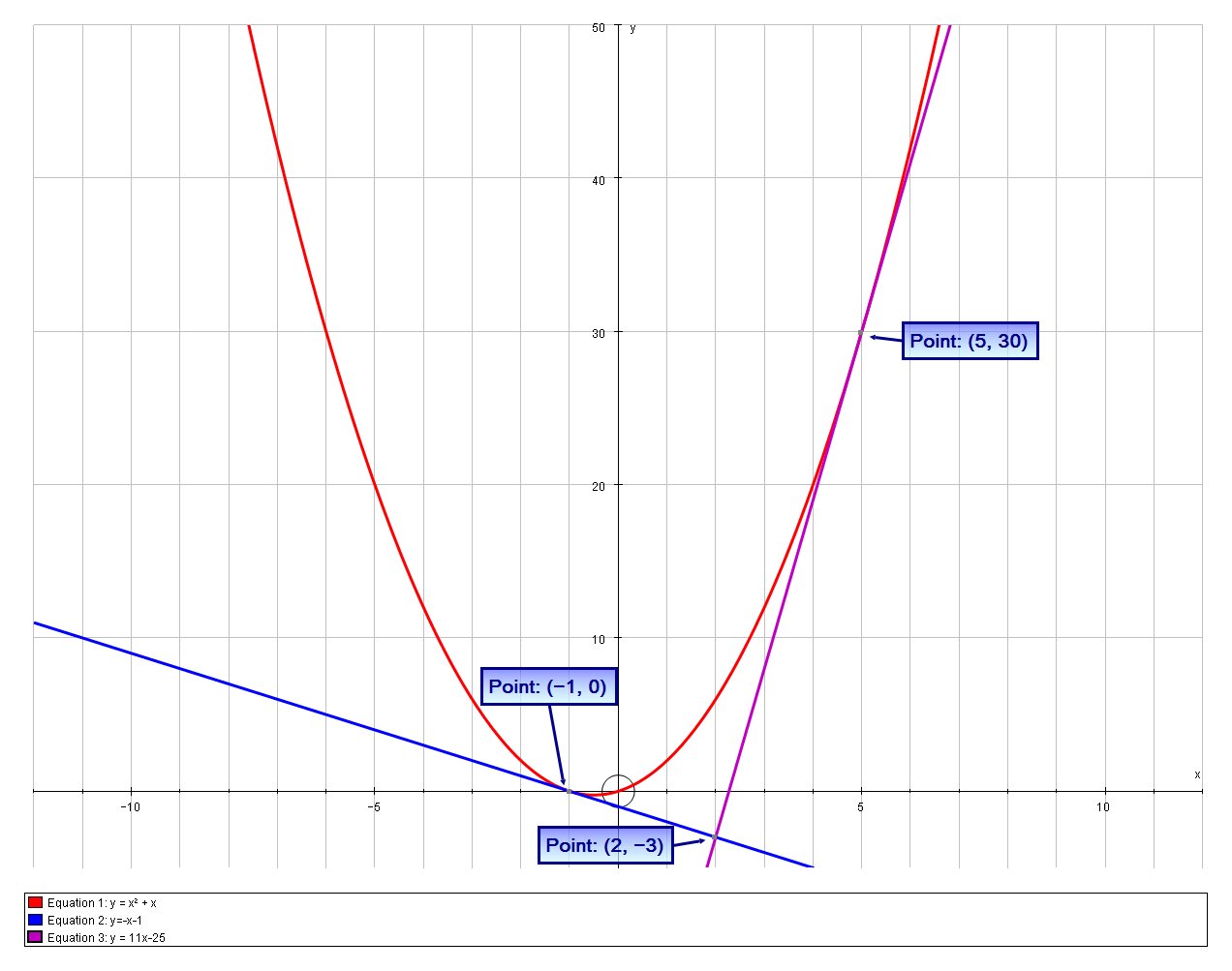
The two tgts. are
Explanation:
Let
Using the Slope-point Form , we get, its eqn.,
Solving this eqn. with
the Parabola with the tgt. line.
But, a tgt. essentially intersects the Parabola in only one pt.,
For
N.B.:
Enjoy Maths.!

