Question

How do you find the height, h of a mountain using the info given in figure 5.2.9?

See http://www.chegg.com/homework-help/find-height-h-mountain-using-information-given-figure-529fig-chapter-5.2-problem-6e-solution-9781449649128-exc for the figure.

Answer 1

`tan(28)/(1-tan(28))` km`~~1.135` km

Explanation:

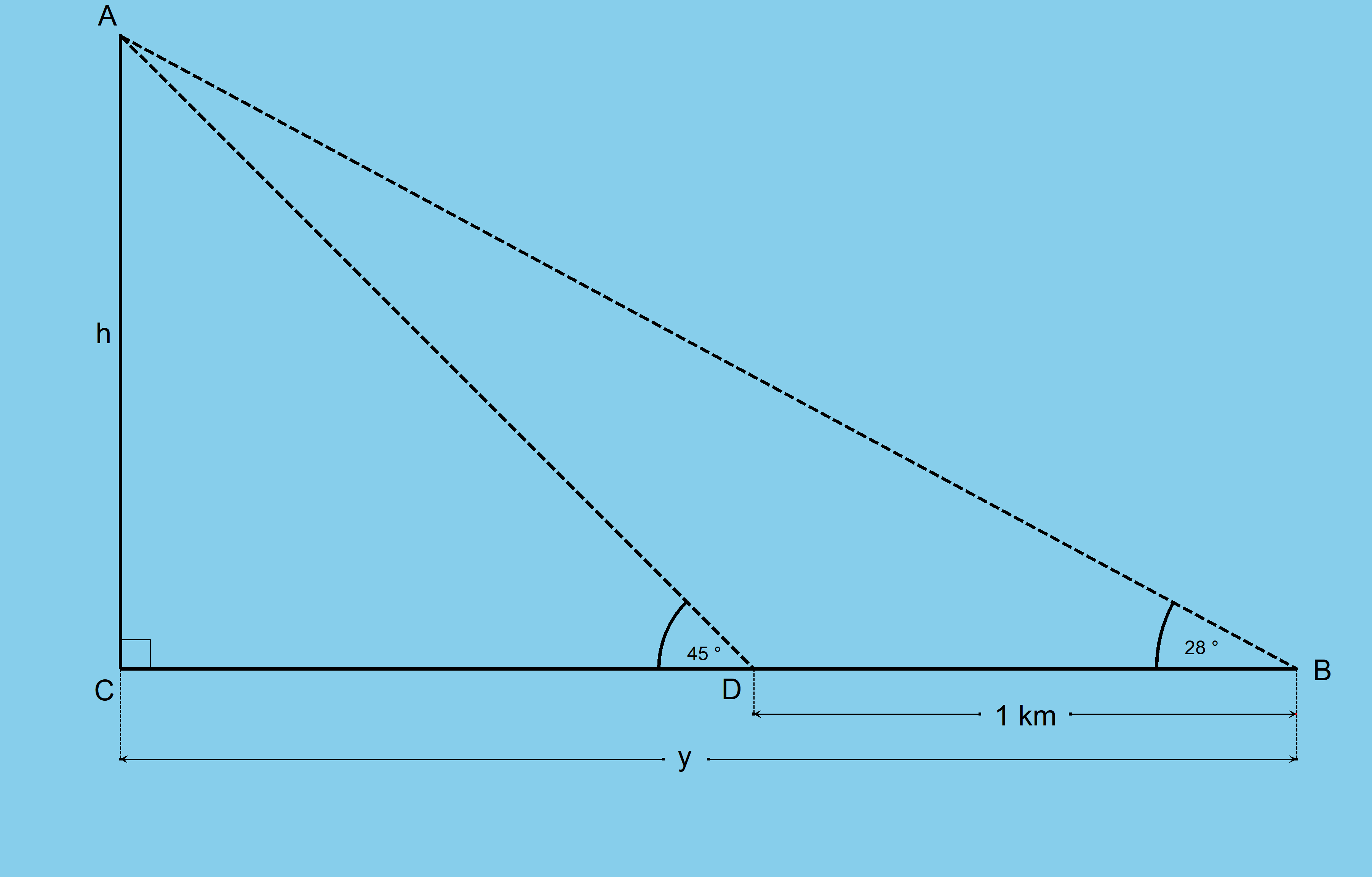
Using the tangent function.

`tan(theta)="opposite"/"adjacent"`

Triangle ABC

`tan(28)=h/y=>h=ytan(28) \ \ \ \ \[1]`

Triangle ADC

`tan(45)=h/(y-1)=h=(y-1)tan(45)`

This means:

`ytan(28)=(y-1)tan(45)`

`(y-1)/y=tan(28)/tan(45)`

`y=1/(1-tan(28)/tan(45))`

Substituting this in `[1]`

`h=tan(28)/(1-tan(28)/tan(45))=(tan(45)tan(28))/(tan(45)-tan(28))`

`tan(45)=1`

`h=tan(28)/(1-tan(28))`

Height of mountain is:

`tan(28)/(1-tan(28))` km`~~1.135` km