Question

How do you find the inscribed circle in a triangle?

Answer 1

See below:

Explanation:

To inscribe a circle in a triangle, you need a compass and a straightedge (or ruler).

Start out by bisecting one of the angles of the triangle (aka, divide it into two equal angles).

To bisect and angle, put your compass on the vertex of the angle (I'm going to use `angle A`), and make an arc:

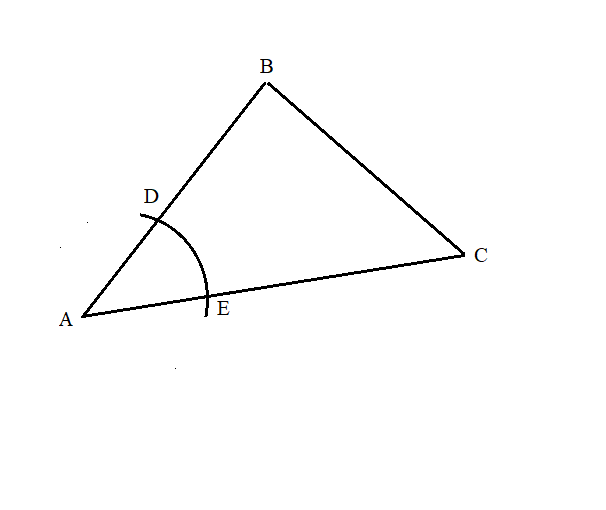
I went ahead and labeled where it intersected `AB` and `AC` with the points `D` and `E`.

Now put your compass on `D` and `E` and make two more tiny arcs, and draw a line from the vertex `A` to where the arc intersect:

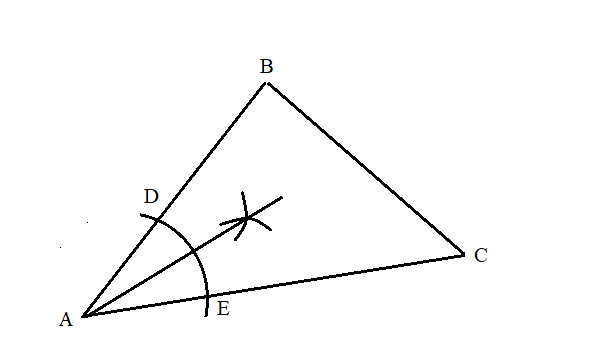
Now do this same thing with another angle. I'm going to use `angleC`:

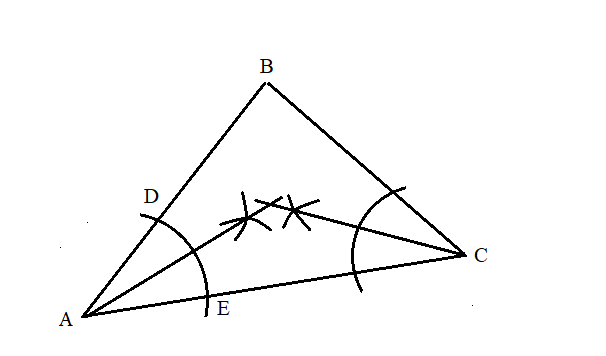
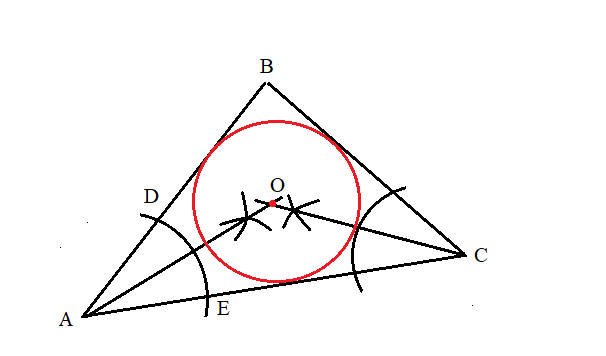
Do you see where those two lines intersect? That's the `"incenter"` of the triangle, meaning point that you can use as the center of the `"incircle"`. Put your compass right where those lines intersect and draw a circle:

Circle `O` is the incircle of of `triangle ABC`.

NOTE: My diagrams are inaccurate. However, the method will always work. I was just using computer software and was unable to use an actual compass - so my attempt is not perfect!