How do you find the instantaneous rate of change of a function at a point?
1 Answer
You can find the instantaneous rate of change of a function at a point by finding the derivative of that function and plugging in the
Instantaneous rate of change of a function is represented by the slope of the line, it tells you by how much the function is increasing or decreasing as the
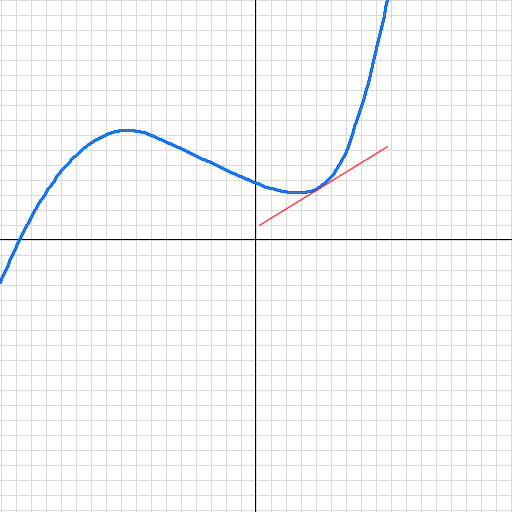
Figure 1. Slope of a line
In this image, you can see how the blue function can have its instantaneous rate of change represented by a red line tangent to the curve. To find the slope of this line, you must first find the derivative of the function.
Ex:
#2x^2+4 , (1,6)#
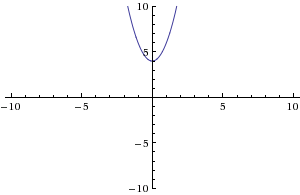
credit: www.wolframalpha.com
Using the power rule for derivatives, we end up with
#4(1) = 4#
This tells us that the slope of our original function at
If we also wanted to find the equation of the line that is tangent to the curve at the point, which is necessary for certain applications of derivatives, we can use the Point-Slope Form:
#y-y_1=m(x-x_1)#
with
Plugging in our
#y-6=4(x-1)#
Which simplifies to
#y=4x+2#
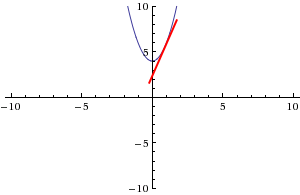
Problems involving "instantaneous rate of change" of a function require you to use the derivative, though it could be disguised in a way you may not be familiar with, such as the velocity of an object after a certain amount of time. Practicing similar rate of change problems will help you get a feel for the practical uses of derivatives.

