How do you find the intercepts of #x^2y-x^2+4y=0#?

2 Answers
Gió
Mar 24, 2015

For the intercepts you set alternately #x=0# and #y=0# in your function:
enter image source here
and graphically:
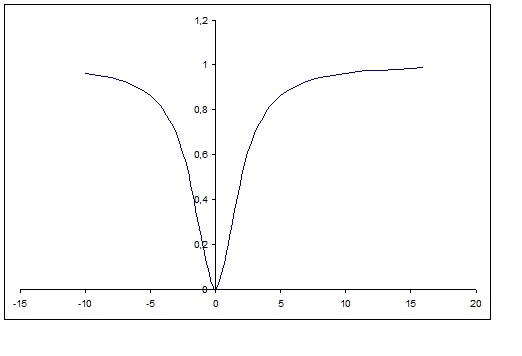
enter image source here

Alan P.
Mar 24, 2015

On the X-axis #y=0#
So
#x^2y -x^2 + 4y = 0#
becomes
#x^2(0) - x^2 + 4(0) = 0#
#rarr -x^2 = 0#
#rarr x = 0#

On the Y-axis #x=0#
and the original equation
#x^2y -x^2 + 4y = 0#
becomes
#(0)^2y -(0)^2 +4y = 0#
#rarr y=0#

The only intercept for the given equation occurs at #(0,0)#

Related questions
See all questions in Intercepts by Substitution
Impact of this question
15568 views around the world
You can reuse this answer
Creative Commons License