How do you find the intervals of increasing and decreasing using the first derivative given #y=-2x^2+4x+3#?
1 Answer
Explanation:
We want to perform that first derivative test here:
We begin by differentiate using the power rule:
Keep in mind that
Now we want to factor and set it equal to zero:
We create a test a interval from
Now you pick numbers in between the interval and test them in the derivative. If the number is positive this means the function is increasing and if it's negative the function is decreasing.
I picked 0 a number from the left
This means from
Then I picked a number from the right which was 2.
This means from
So, from
Note: For this exact reason we can say that there's an absolute max at
Attach is an image that may help you:
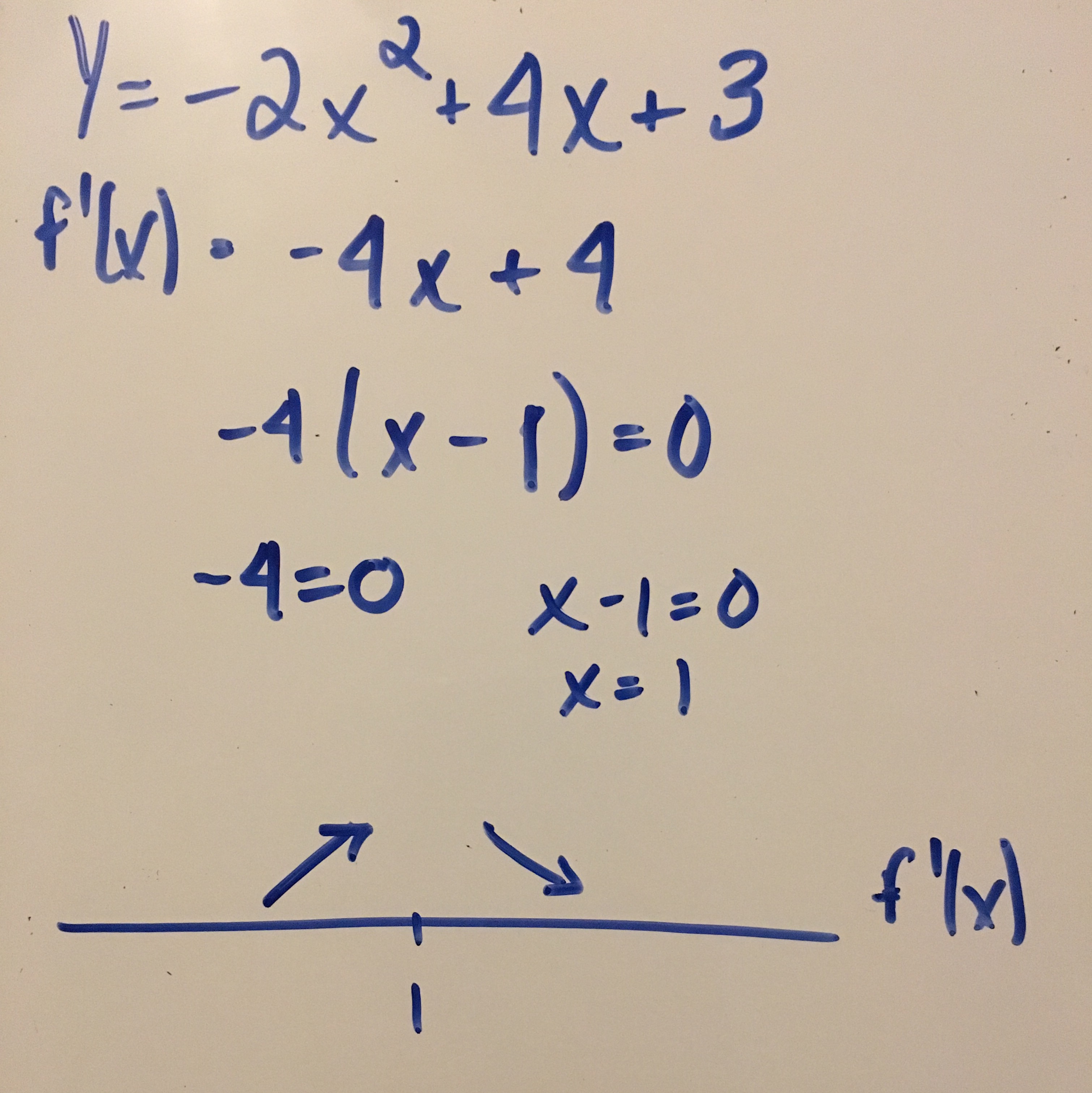
The graph will help you visualize it better.
graph{-2x^2+4x+3 [-10, 10, -5, 5]}

