Question

How do you find the intervals of increasing and decreasing using the first derivative given `y=cos^2(2x)`?

Answer 1

#y " is" { ("increasing", =>, pi/4 < x < pi/2, (3pi)/4 < x < pi, ...), ("stationary", =>, x=0, x=pi/4, ...), ("decreasing", =>, 0 < x < pi/4, pi/2 < x < (3pi)/2, ..) :} #

Explanation:

`y=cos^2(2x)` is # { ("increasing", <=>, dy/dx> 0), ("stationary", <=>, dy/dx= 0), ("decreasing", <=>, dy/dx< 0) :} #

Differentiating wrt `x` we have:

`dy/dx = 2cos(2x)(-sin(2x))(2)`
`:. dy/dx = -4cos(2x)sin(2x)`
`:. dy/dx = -2sin(4x)`

This is the graph of the derivative :

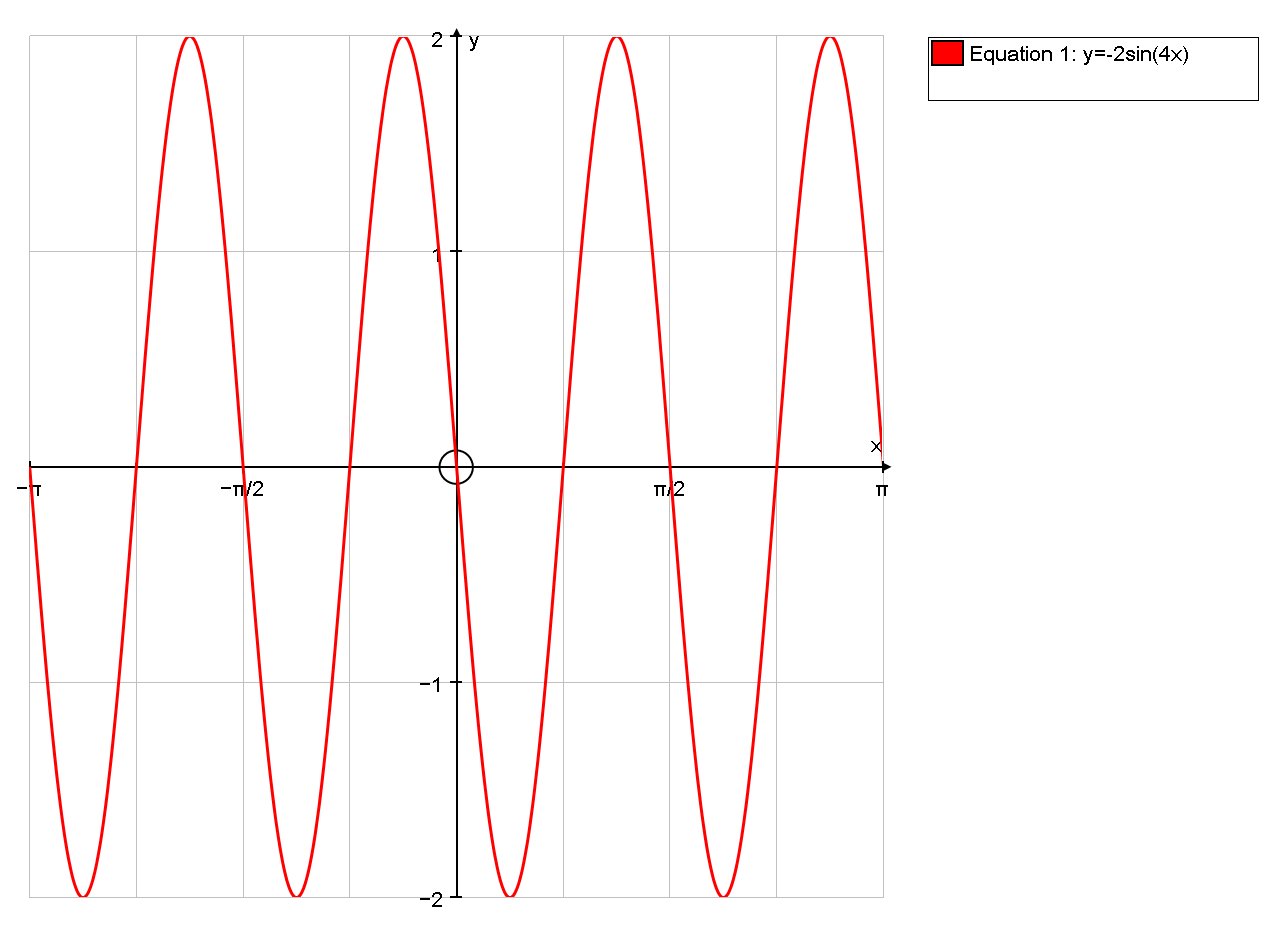
#y " is" { ("increasing", =>, pi/4 < x < pi/2, (3pi)/4 < x < pi, ...), ("stationary", =>, x=0, x=pi/4, ...), ("decreasing", =>, 0 < x < pi/4, pi/2 < x < (3pi)/2, ..) :} #