Question

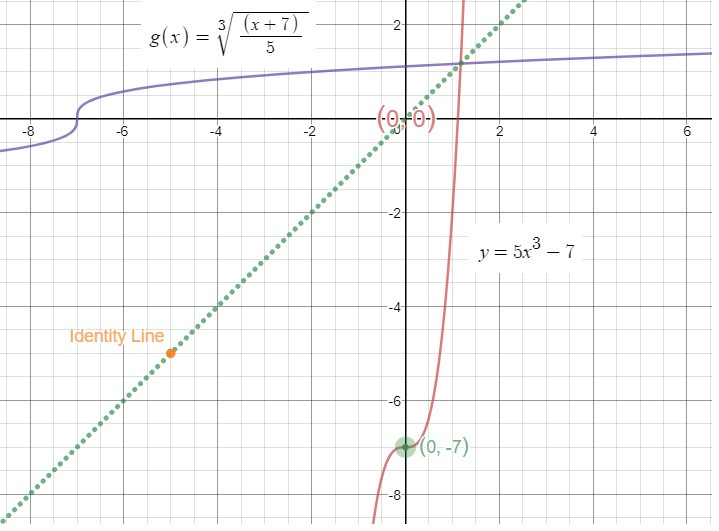
How do you find the inverse of `f(x) = 5x^3 - 7`?

Answer 1

`" "`
Inverse of the function `color(red)(f(x)=5x^3-7` is given by `color(blue)(root(3)((x+7)/5`

Explanation:

`" "`

Note:

The Inverse of a function may NOT always be a function.

So, if the inverse of a function is a function by itself, then it is called an Inverse Function.

How do we determine these inverse relationships ?

Method 1

We can find the inverse of the function by simply swapping the ordered pairs.

Method 2

(a) Set the function to `y`

(b) Swap the `x`, `y` variables

(c) Solve for `y`

Method 3

The graph of an inverse function is the reflection of the original graph over the line `color(red)(y=x`, called the Identity Line.

`color(green)("Step 1 : "`

Given the function : `color(red)(y=f(x)=5x^3-7`

Construct a data table for this function and graph it.

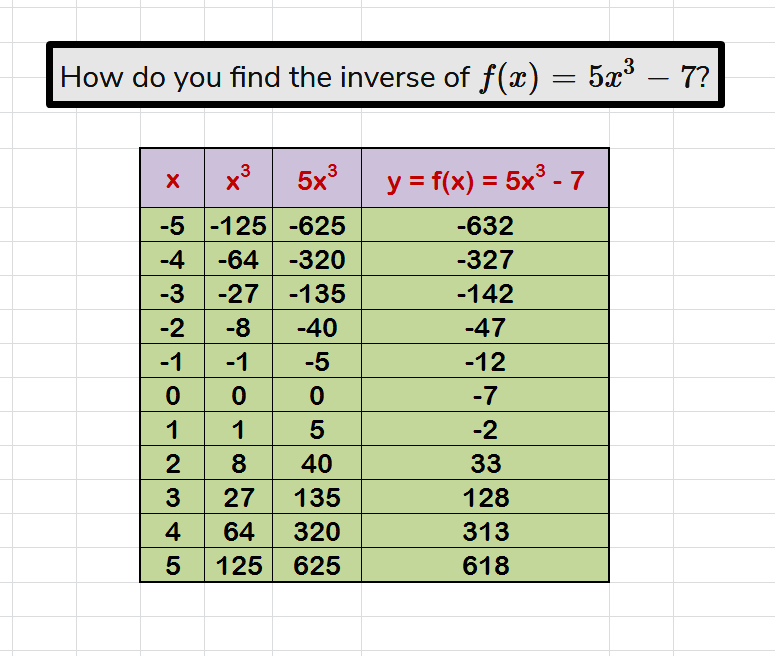
Behavior of the Parent Graph shown

`color(green)("Step 2 : "`

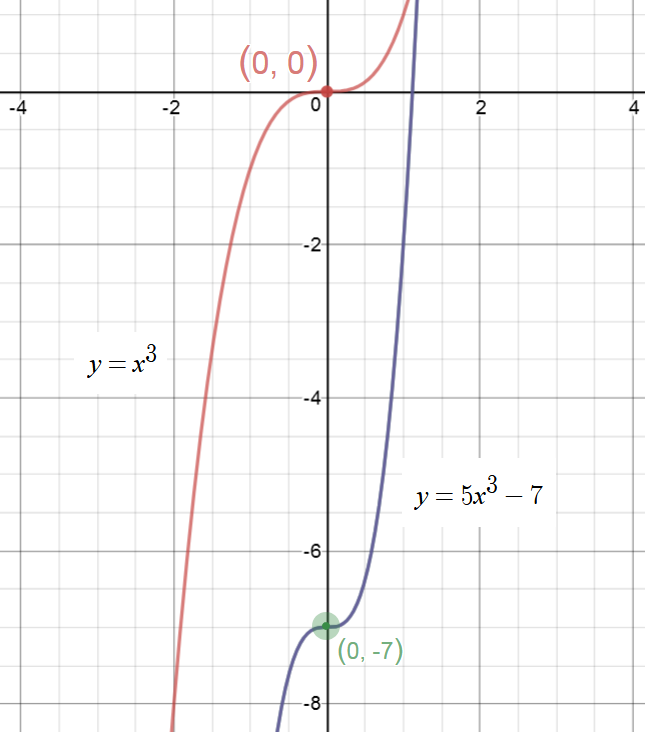
We use the Method 2 to solve

(a) Set the function to `y`

`y= 5x^3-7`

(b) Swap the `x`, `y` variables

`x=5y^3-7`

(c) Solve for `y`

We have, `x=5y^3-7`

Subtract `5y^3` from both sides.

`rArr x-5y^3=5y^3-7-5y^3`

`rArr x-5y^3=cancel (5y^3)-7-cancel(5y^3)`

`rArr x-5y^3=-7`

Subtract `x` from both sides

`rArr x-5y^3-x=-7-x`

`rArr cancel x-5y^3-cancel x=-7-x`

Multiply both sides by `(-1)` to remove negative signs.

`rArr (-1)(-5y^3)=(-1)(-7-x)`

`rArr 5y^3=7+x`

`rArr 5y^3=x+7`

Divide both sides by `5`

`rArr (5y^3)/5=(x+7)/5`

`rArr (cancel 5y^3)/cancel 5=(x+7)/5`

`y^3=(x+7)/5`

Take Cube Root on both sides

`rArr root(3)(y^3)=root(3)[(x+7)/5]`

Cube and the Cube Root cancel each other.

`rArr y=root(3)[(x+7)/5]`

Hence,

Inverse of the function `color(red)(f(x)=5x^3-7` is given by `color(blue)(root(3)((x+7)/5`

`color(green)("Step 3 : "`

Explore the graph: