By Chain Rule,
#{dr}/{d theta}=3cos^2(theta/3)cdot[-sin(theta/3)]cdot1/3#
by cleaning up a bit,
#=-cos^2(theta/3)sin(theta/3)#
Let us first look at the curve #r=cos^3(theta/3)#, which looks like this:
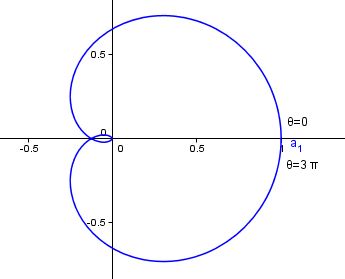
Note that #theta# goes from #0# to #3pi# to complete the loop once.
Let us now find the length #L# of the curve.
#L=int_0^{3pi}sqrt{r^2+({dr}/{d theta})^2} d theta#
#=int_0^{3pi}sqrt{cos^6(theta/3)+cos^4(theta/3)sin^2(theta/3)}d theta#
by pulling #cos^2(theta/3)# out of the square-root,
#=int_0^{3pi}cos^2(theta/3)sqrt{cos^2(theta/3)+sin^2(theta/3)}d theta#
by #cos^2theta=1/2(1+cos2theta)# and #cos^2theta+sin^2theta=1#,
#=1/2int_0^{3pi}[1+cos({2theta}/3)]d theta#
#=1/2[theta+3/2sin({2theta}/3)]_0^{3pi}#
#=1/2[3pi+0-(0+0)]={3pi}/2#
I hope that this was helpful.

