How do you find the limit of #x/sinx# as x approaches 0?
4 Answers
Explanation:
Let
Explanation:
We need to know the important trigonometric limit:
#lim_(xrarr0)sinx/x=1#
So, we see that:
#lim_(xrarr0)x/sinx=lim_(xrarr0)(sinx/x)^-1=(lim_(xrarr0)sinx/x)^-1=1^-1=1#
Explanation:
If we try to calculate the limit directly, we can see that is an indeterminate form:
To solve it, we can apply the L'Hôpital's rule:
Given two functions
If
So we have:
NOTE
The question was posted in "Determining Limits Algebraically" , so the use of L'Hôpital's rule is NOT a suitable method to solve the problem. Therefore this solution is invalid.
ANSWER TO THE NOTE
This limit can not be solved using only algebraic concepts as the function
The answer above that uses the limit
I think the person who wrote the first note confuses the term "algebraic" in the expression "Determining Limits algebraically" in the true meaning of the word algebraic, regardless of that expression usually means "Determination of limits analytically", ie, by calculation and not graphically, numerically (using approximations) or intuitive.
Use the squeeze theorem;
Explanation:
We can use the squeeze theorem (or sandwich theorem), which states that if
So the challenge is to find upper and lower bounds for
Consider:
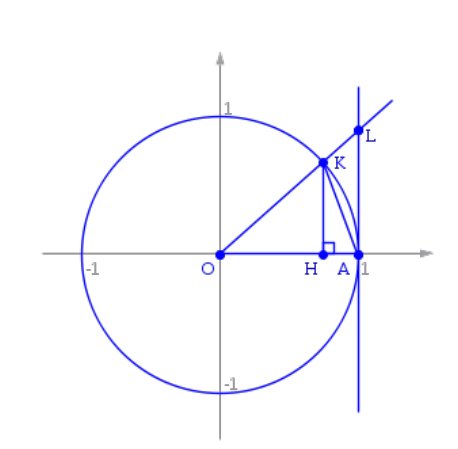
We have:
{Area of
Multiplying by
Hence, by the squeeze theorem,




