Question

How do you find the limits of the function below?

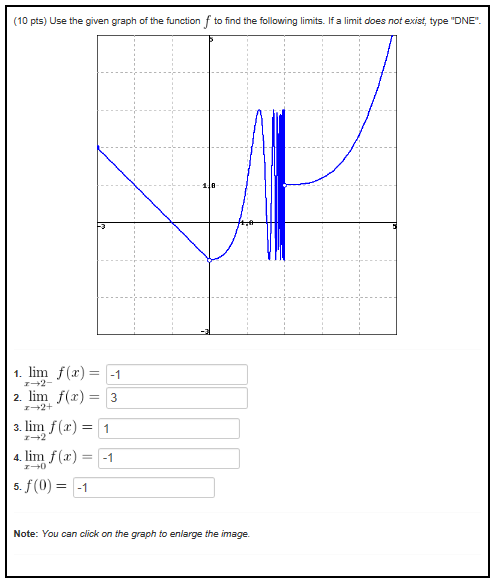We were assigned a whole bunch of homework for the Thanksgiving Break, and to my surprise, we've stopped doing trig and moved into calculus. We've had no discussion or previous exposer to these types of problems, so I'm just blindly trying to figure out what's going on. Mostly I'm just confused between the difference between "x->2" "x->2-" and "x->2+". Also, all answers have to be correct for the website this is on to take it, so can someone please tell me which of my answers are right and which I need to look over again? I'm lost and don't really know what I'm doing.

Answer 1

Please see below.

Explanation:

Hi Sarah,

I can't see clearly what the graph is doing at x=2. When you approach 2 from the negative direction does the function go to 3, -1? whichever it goes to is the limit from the negative direction.

The limit when x goes to 2 from the positive direction seems to be 1 because that is the value of y it is going towards.

The limit when x goes to 2 does not exist because at x=2 you get different values for the function depending on which direction you come from. For the limit to exist when x goes to 2, you would need to get the same value for the limits from the positive and negative directions.

The answer to number 1 is either `3` or `-1` depending on which one the graph goes to.

The answer to number 2 is `1` because that is the value the function goes toward even though there is a hole at `x=2`.

The answer to number 3 is `DNE` because you get different values for the function as you approach `2` depending on which direction you come from. For this limit to exist you would have to get the same value from both directions.

The answer to number 4 is correct at `-1`.

The answer to number 5 is `DNE` because your function does not exist at that value. You have a hole.