Question

How do you find the local maximum and minimum values of `f(x) = x / (x^2 + 81)` using both the First and Second Derivative Tests?

Answer 1

Minimum `(-9,-1/18)` , Maximum `(9,1/18)`

Explanation:

`f(x)=x/(x^2+81)`

`D_f=RR`

• `f'(x)=(x^2+81-x(2x))/(x^2+81)^2` `=`

`(-x^2+81)/(x^2+81)^2` `=`

`-(x^2-81)/(x^2+81)^2`

`f'(x)=0` `<=> x^2-81=0 <=> x^2=81 <=> (x=9 or x=-9)`

Let's plug in `f'` a value , `x_1in` `(-9,9)` . For example, for `x_1=0`
we get

`f'(0)=-(-81)/81^2=81/81^2>0`

Let's plug in `f'` a value which is `>9` . For example, for `x_2=10`
we get

`f'(10)=-(100-81)/(100+81)^2=-19/181^2<0`

Let's plug in `f'` a value which is `<-9` . For example, for `x_3=-10`
we get

`f'(-10)=-(100-81)/(100+81)^2=-19/181^2<0`

As a result we have:

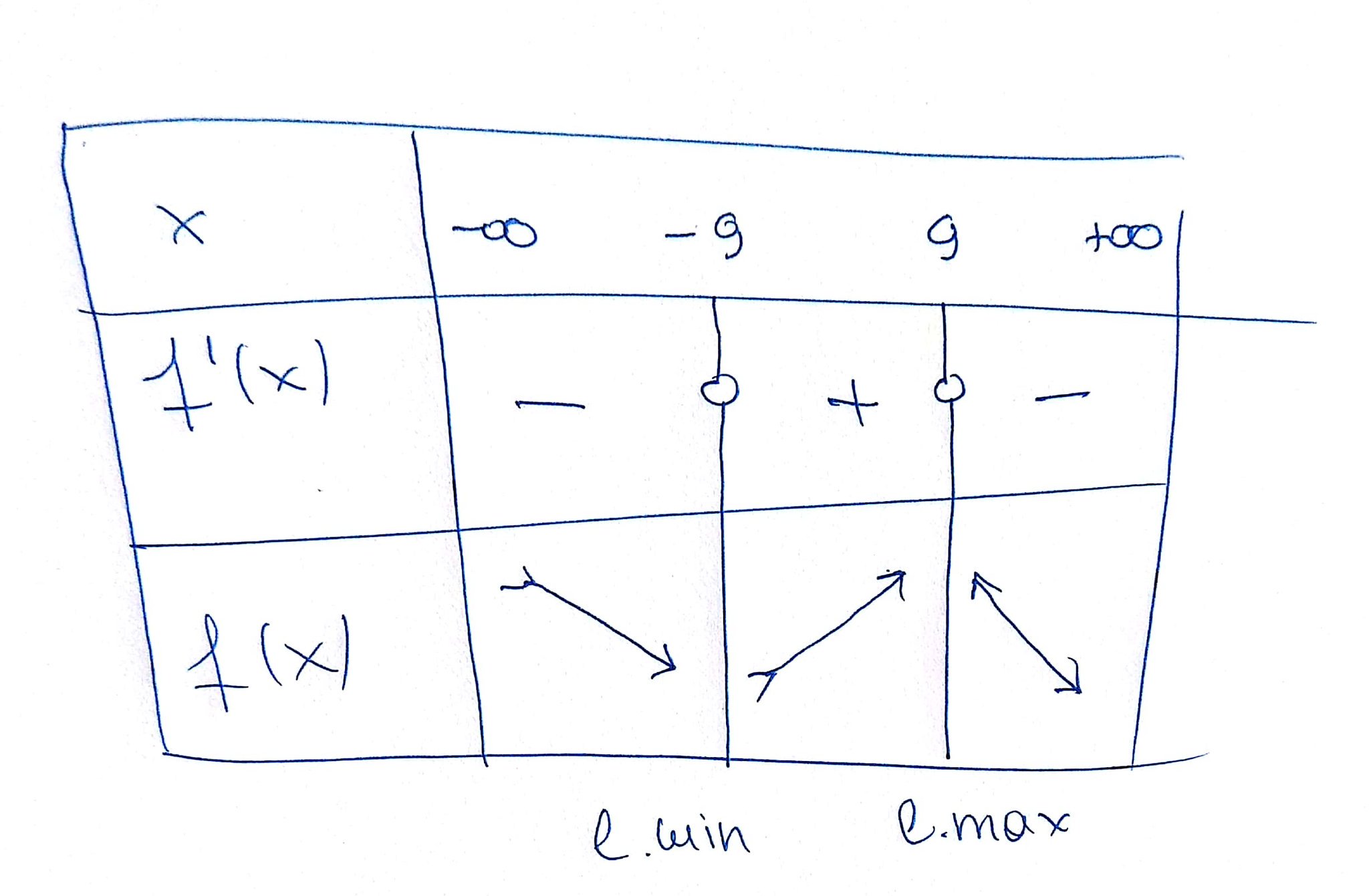
• `f` continuous in `(-oo,-9]` and `f'(x)<0` for `x` `in` `(-oo,-9)`
  so `f` is strictly decreasing in `(-oo,-9]`

• `f` continuous in `[-9,9]` and `f'(x)>0` for `x` `in` `(-9,-9)`
  so `f` is strictly increasing in `[-9,9]`

• `f` continuous in `[9,+oo)` and `f'(x)<0` for `x` `in` `(9,+oo)`
  so `f` is strictly decreasing in `[9,+oo)`

`f` is decreasing in `(-oo,-9]` and increasing in `[-9,9]`
therefore `f` has a local minimum at `x=-9`

`f` is increasing in `[-9,9]` and decreasing in `[9,+oo)`
therefore `f` has a local maximum at `x=9`