Question

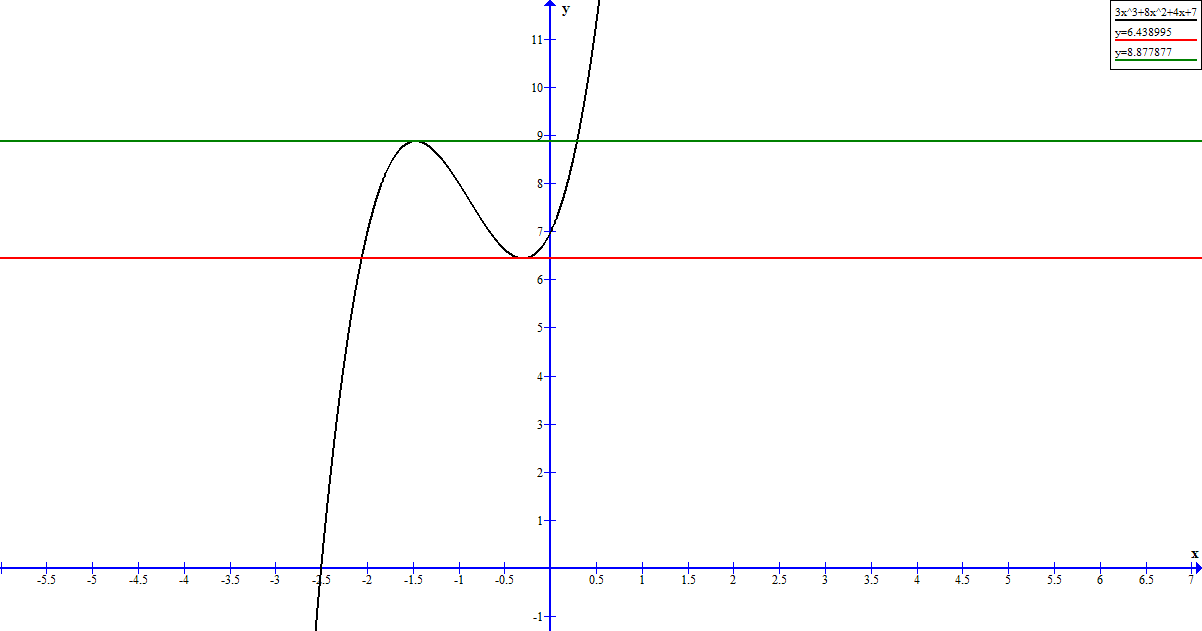
How do you find the points where the graph of the function # f (x) = 3 x^ 3 + 8 x^ 2 + 4 x + 7 # has horizontal tangents and what is the equation?

Answer 1

Horizontal tangent equations:
`color(white)("XXX")color(green)(f(x)=6.438995)` at `color(green)(""(-0.30094,6.438995))`
`color(white)("XXX")color(green)(f(x)=8.877877)` at `color(green)(""(-1.47683,8.877877))`

Explanation:

The slope of the tangent is given by the derivative of the function.

Given
`color(white)("XXX")f(x)=3x^3+8x^2+4x+7`
the slope of the tangent for a general value of `x` is
`color(white)("XXX")f'(x)=9x^2+16x+4`

The tangent is horizontal when the slope is equal to zero.

`color(white)("XXX")9x^2+16x+4=0` for values of `x` where the tangent is horizontal

Using the quadratic formula, we have
`color(white)("XXX")x=(-16+-sqrt(16^2+4xx9xx4))/(2xxx9)=(-8+-2sqrt(7))/9`

Using a calculator, we get (approximate) values
`color(white)("XXX")x=-0.30094` and `x=-1.47683`

Plugging each of these values for `x` into the original equation
gives corresponding values for `f(x)`
`color(white)("XXX")f(x)=6.438995` and `f(x)=8.877877`
which are the equations of the corresponding horizontal lines.

Here is a graph of the original function and the tangent lines derived above which supports this answer: