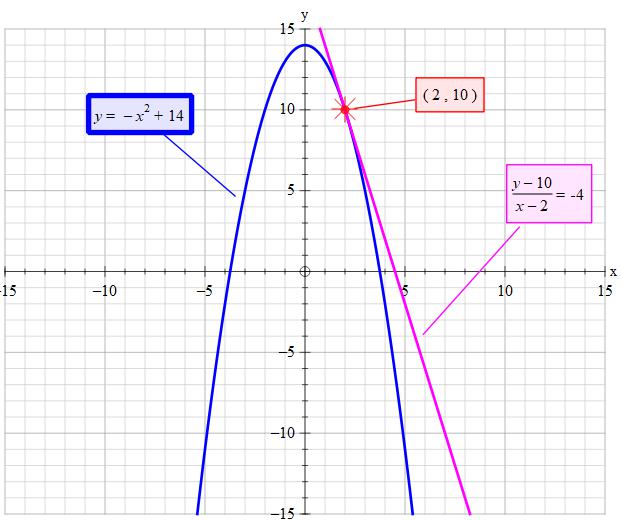
How do you find the slope of a tangent line to the graph of the function #g(x) = 14 − x^2# at (2, 10)?
3 Answers
Explanation:
#"the slope of the tangent line "=f'(2)#
#f'(x)=-2x#
#f'(2)=-2(2)=-4larrcolor(blue)"slope of tangent line"#
Part 2 of 2
Using FIRST PRINCIPLES with explanation about determining the slope
Explanation:
Slope (gradient) is
Suppose we have two points on the graph.
Let the first point be
Let the second point be
Then
This you should have seen before!
In Calculus you start to bring the two points so close together that you can not physically measure the gap between them.
Suppose instead of using
These days people use
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Set the fist point as
Let the next point progress by some minuscule value in
Set
Then the progression point gives us:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
But we need the gradient which is
but change in
We now make
Part 1 of 2
Using shortcut:
Explanation:
Given point
Set
If we have
The constant of
So in this case:
The slop
In other words it is the UNIT RATE OF CHANGE.
So at