Question

How do you find the slope of the tangent line to the graph of `y = (ln x) e^x` at the point where x = 2?

Answer 1

The slope of the tangent is `f'(2) = e^2ln2+1/2e^2`

Explanation:

The gradient of the tangent to a function at any particular point is given by the derivative of the function at that point.

Differentiating `y = (lnx)e^x` wrt `x` ( using the product rule) we get:

`\ \ \ \ \ dy/dx = (lnx)(d/dxe^x) + (d/dxlnx)(e^x)`
`:. dy/dx = (lnx)e^x + (1/x)(e^x)`
`:. dy/dx = ((lnx)+1/x)e^x`

When `x=2` we have;

`f'(2) = ((ln2)+1/2)e^2 = e^2ln2+1/2e^2`

If we wanted to find the equation of the tangent:

`\ \ f(2) =(ln2)e^2 = e^2ln2`

So the tangent we seek passes through `(2, e^2ln2)` and has slope `e^2ln+1/2e^2`, so using `y-y_1=m(x-x_1)` the equation is;

`y - e^2ln2 = (e^2ln2+1/2e^2 )(x-2)`
`:. y - e^2ln2 = (e^2ln2+1/2e^2 )x-2(e^2ln2+1/2e^2 )`
`:. y - e^2ln2 = (e^2ln2+1/2e^2 )x-2e^2ln2-e^2`
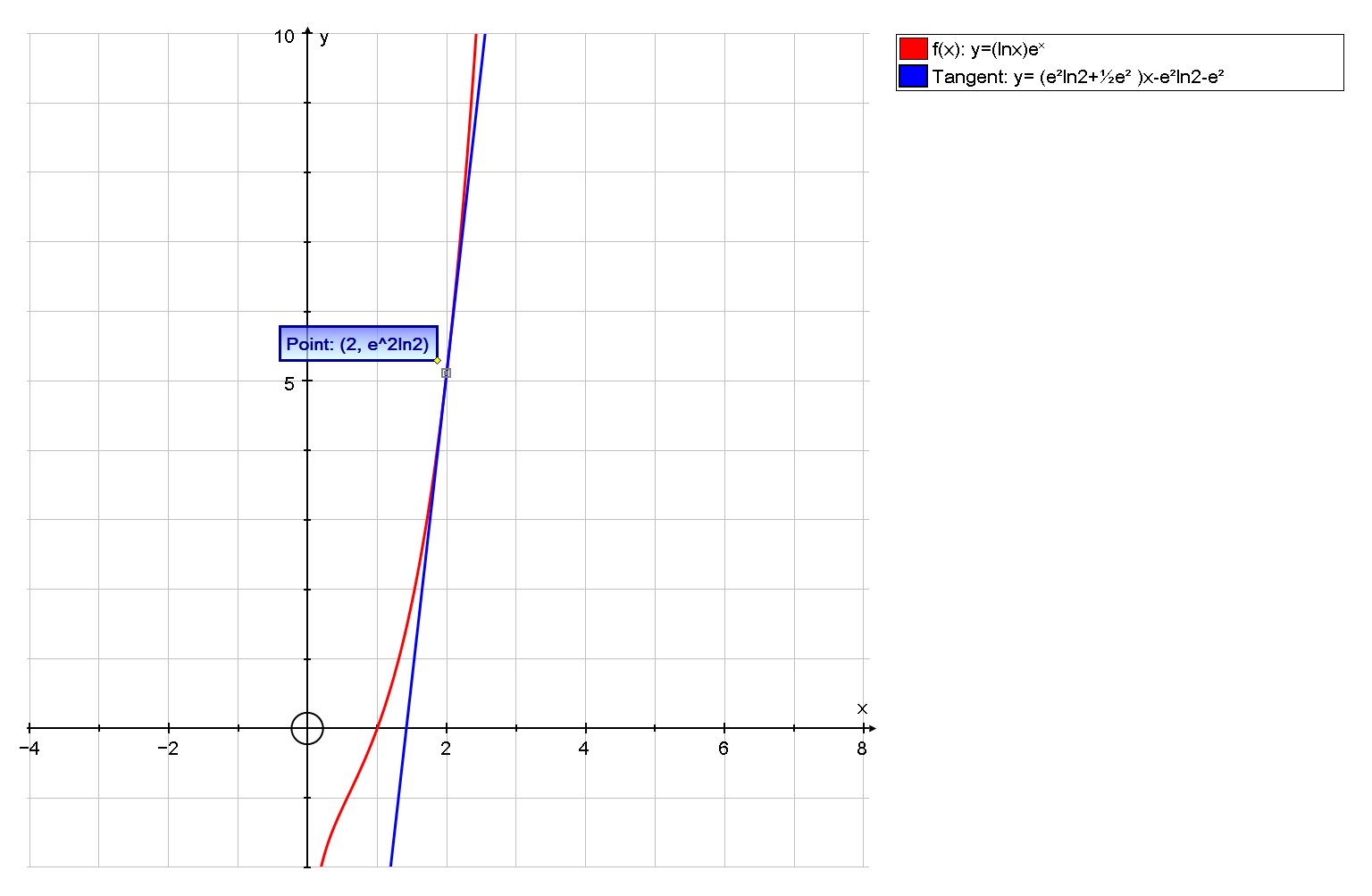
`:. y= (e^2ln2+1/2e^2 )x-e^2ln2-e^2`

We can verify this is correct by the following graph: