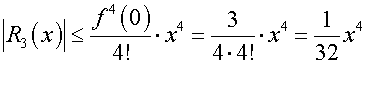Question

How do you find the Taylor remainder term `R_3(x;0)` for `f(x)=1/(2+x)`?

Answer 1

This exact value of `R_n(x)` is

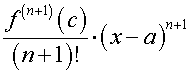
for some value of `c` between `a` and `x`

However we can determine an upper bound for `R_3(x)`

which is

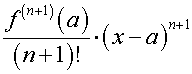
Hence for `a=0` and `n=3` we get

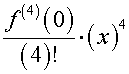
where

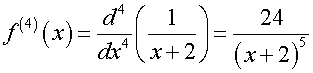
hence

`f^4(0)=24/2^5=3/4`

So finally we have that