How do you find the volume bounded by #x=8-y^2# and #x=y^2# revolved about the y-axis?
1 Answer
Explanation:
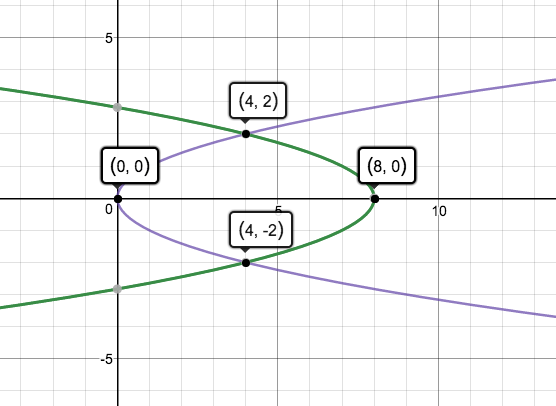
There are a number of more traditional ways to do this but I would recommend Pappus' [2nd] Theorem...
....which states that the volume V of a solid of revolution generated by the revolution of a lamina about an external axis is equal to the product of the area A of the lamina and the distance travelled by the lamina's geometric centroid.
To b specific, the shape in the graph has, due to all the symmetry, its geometric centroid at (4,0). And the centroid will travel a distance of
That's in 1 revolution about the y-axis
In terms of the lamina's area, we can be equally frugal by noting the symmetry. All we need is the area of one quarter of the shape shown in the graph so that the total area A is
So the blue line represents
So

