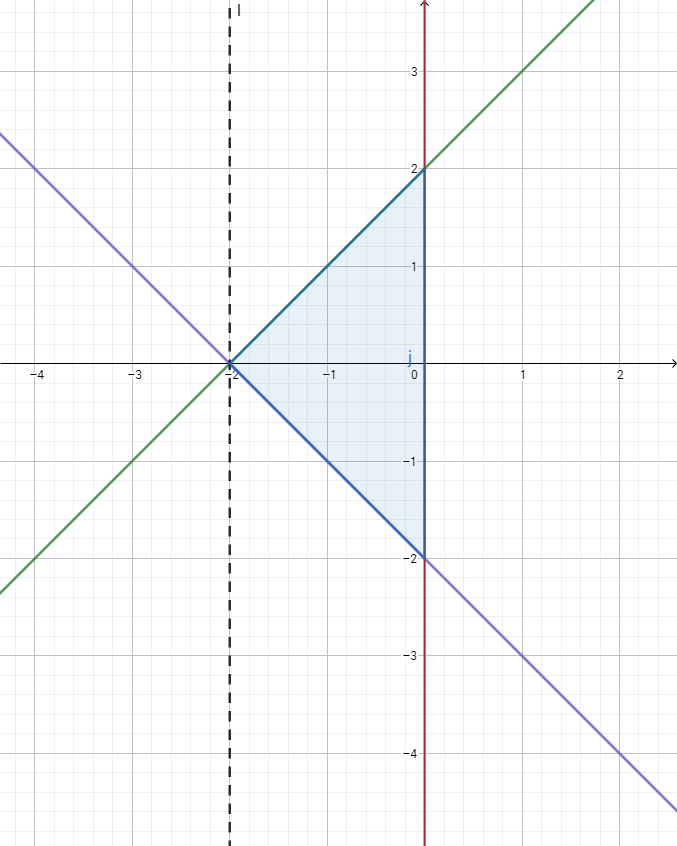
How do you find the volume bounded by y=x+2, y=-x-2 and x=0 revolved about the x=-2?
1 Answer
Explanation:
Since this is a revolution about a vertical line (
Looking at the region to be revolved (graph below), it should be noted that the top half of the region is symmetric to the bottom half; both will sweep out the same shape (albeit inverted). Thus, we only have to find the volume of the top half and we can double it to get the final volume.
Since the top half will have an empty space in the center, this will require an integration that "subtracts" out volume. The general form of the formula for the volume in this instance is:
By examining the graph, the outer radius is fixed at 2 (the distance from
The volume, keeping in mind we have to double this volume to account for the bottom half. is then:
Method 2 - Analytical Geometry
By looking at the region to be rotated, the volume can be described as a cylinder with an hourglass shape carved out of the middle of it (2 cones touching nose to nose). Knowing this, you can avoid integration and use volume formulas instead: